Trucos SAS. Medir la importancia de las variables en nuestro modelo de regresión logística

Hoy quería proponeros una forma poco ortodoxa de medir la importancia de las variables en un modelo de regresión logística con SAS. La cuestión es: dado un modelo de regresión logística crear un ranking con las variables más importantes dentro del modelo. Para esta tarea recomiendo el uso de random forest, pero puede ser imposible disponer de un software que realice este tipo de modelos. Imaginemos un caso concreto, disponemos de SAS STAT y nos da reparo trabajar con R. Para este caso podemos emplear el siguiente truco. El AIC (criterio de información de Akaike) es un estadístico que relaciona el cociente de la verosimilitud con el número de parámetros del modelo que ajustamos. Cuanto menor sea este cociente mejor será nuestro modelo. Si eliminamos una variable del modelo ¿cuánto empeora este modelo? Esa será la filosofía que emplearemos para analizar la importancia de las variables presentes en nuestro modelo. En la línea habitual hacemos un ejemplo para que podáis copiar y pegar en vuestro SAS:

Vamos a crear un dataset preparado para hacer una regresión logística perfecta donde en un 10% de los casos sucede un evento:

*REGRESION LOGISTICA PERFECTA;
data logistica;
do i=1 to 10000;
  normal1=rannor(8);
  normal2=rannor(45);
  normal3=rannor(32);
  normal4=rannor(7);
  normal5=rannor(98);
  unif1=ranuni(2);
  unif2=ranuni(21);
  unif3=ranuni(22);
  unif4=ranuni(23);
  unif5=ranuni(24);
  prob=1/(1+exp(-(-3.16+0.1*normal1-0.2*normal2+0.3*normal3-0.4*normal4+0.5*normal5+
	   0.1*unif1+0.2*unif2+0.3*unif3+0.4*unif4+0.5*unif5)));
  sucede=ranbin(8,1,prob);
  *TRAMIFICAMOS LAS VARIABLES;
  normal1=round(rannor(8),0.1);
  normal2=round(rannor(45),0.2);
  normal3=round(rannor(32),0.3);
  normal4=round(rannor(7),0.4);
  normal5=round(rannor(98),0.5);
  unif1=round(ranuni(2),0.1);
  unif2=round(ranuni(21),0.2);
  unif3=round(ranuni(22),0.3);
  unif4=round(ranuni(23),0.4);
  unif5=round(ranuni(24),0.5);
  output;
end;
drop i;
run;

title "Logistica con un 10% aprox de casos positivos";
proc freq data=logistica;
tables sucede;
quit;

Incialmente necesitamos las variables presentes en el modelo y el ajuste inicial, también un conjunto de datos SAS con los nombres de las variables. Esto es un poco chapuza, pero si seguís el blog podéis hacer este código mucho más elegante [no os lo voy a dar todo hecho]:

*VARIABLES QUE QUEREMOS ESTUDIAR EN EL MODELO;
%let lista_var = normal1 normal2 normal3 normal4 normal5 
	  		 unif1 unif2 unif3 unif4 unif5;

*AJUSTE CON TODAS LAS VARIABLES;
ods output FitStatistics=ajuste_total;
ods results;
proc logistic data=logistica;
class &lista_var.;
model sucede = &lista_var./rsquare ;
quit;

data v1;
input var $;
orden = _n_;
datalines ;
normal1 
normal2 
normal3 
normal4 
normal5 
unif1 
unif2 
unif3 
unif4 
unif5
;run;

Esto es lo primero que necesitamos. Una macro con todas las variables presentes en el modelo, que también metemos en un conjunto de datos SAS que necesita un campo ORDEN y el ajuste con todas las variables. En el ODS pedimos crear un conjunto de datos con los FITSTATISTIC que llamamos ajuste_total. Tendremos un conjunto de datos con 3 observaciones y 3 criterios para medir la bondad del ajuste por máxima verosimilitud de nuestro modelo logístico. Los criterios son el AIC, el SC (Schwarz Criterion) y el -2 Log L que es el contraste del logaritmo de máxima verosimilitud (no sé como traducirlo). Ahora vamos a emplear una macro para hacer todos los modelos posibles con 9 variables, almacenamos los estadísticos de contraste y podemos ver como se “desinflan” cuando eliminamos esa variable. Para ello hacemos una macro muy simple que se puede mejorar [tenéis que trabajar vosotros]:

%macro importance;
*HAY QUE PONER EL NUMERO DE VARIABLES;
%do i = 1 %to 10;
proc sql ; 
select var into: nombre
from v1
where orden = &i.;

select var into: lista_var2 separated by " " 
from v1
where orden ne &i.;
quit;

ods output FitStatistics=ajuste_sin_&nombre.;
proc logistic data=logistica;
class &lista_var2.;
model sucede = &lista_var2./Rsquare ;
quit;

data ajuste_sin_&nombre.;
set ajuste_sin_&nombre.;
eliminada="&nombre.";
rename InterceptAndCovariates = efecto;
run;
%end;
%mend;

%importance;

Esta macro es un bucle que crea una lista de variables excluyendo de una en una a partir del campo orden, esto nos permite hacer los 9 modelos eliminando una variable cada vez, ¿sencillo no? Y a cada ejecución hemos creado un dataset ajuste_sin_VARIABLE SELECCIONADA que contiene el resultado de los ajustes en una variable que denominamos EFECTO. Ahora sólo nos queda juntar todos las tablas con los criterios aunque nos vamos a quedar sólo con el AIC y ordenar para ver que variable tiene más influencia sobre nuestro modelo:

data totales;
set 
ajuste_total
ajuste_sin_normal1
ajuste_sin_normal2
ajuste_sin_normal3
ajuste_sin_normal4
ajuste_sin_normal5
ajuste_sin_unif1
ajuste_sin_unif2
ajuste_sin_unif3
ajuste_sin_unif4
ajuste_sin_unif5;
if criterion="AIC";
run;

proc sort data=totales;
by efecto;
run;

Vale que es una chapuza lo que habéis visto hoy aquí. Pero tiene su rigor. Aunque he de insistir en que es un mecanismo para medir la importancia de una variable DENTRO DE UN MODELO. Es decir, el modelo ya está creado, no es un paso previo a la creación del modelo. Ahora quiero que miréis los resultados obtenidos:

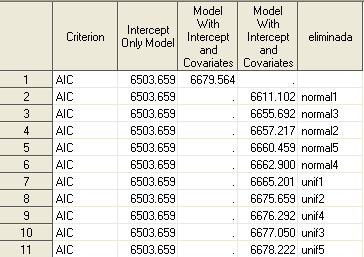
Son curiosos, las variables aleatorias normales aportan más al modelo. Es evidente que la que está más tramificada es la que más aporta al modelo, sin embargo para el resto no es tan claro que un mayor número de niveles implique un mejor comportamiento en el modelo, es un resultado interesante que da pie a otro tipo de análisis que haré más adelante. Saludos.