Regresión PLS con R

El tema que estoy estudiando estos días es la regresión por mínimos cuadrados parciales, partial least squares (PLS). Para documentarme teóricamente y conocer las principales posibilidades de R estoy empleando este documento. Para argumentar el uso de esta técnica de nuevo partimos del modelo lineal general Y = X • Beta + Error donde Beta = inv(X’X) * X’Y y ya analizamos los trastornos que nos provoca la inv(X’X) cuando hay columnas de X que son linealmente dependientes, cuando hay multicolinealidad. En ese caso empleábamos la regresión ridge. Bueno, imaginemos esta situación, tenemos más variables que observaciones. Entonces si que no somos capaces de tener una solución para la inv(X’X). Para este problema contamos con los mínimos cuadrados parciales.

Como siempre se trata de estimar Y a partir de X con la salvedad de que X tiene más columnas que filas y el modelo de mínimos cuadrados ordinarios no tiene solución. En este caso lo primero que se nos puede ocurrir es realizar un análisis de componentes principales de X para reducir la dimensionalidad. Estaríamos ante la regresión por componentes principales, principal components regression (PCR). Esta técnica está íntimamente ligada a la PLS. Lo que haremos será estimar Y a partir de las componentes principales de X. Por definición las componentes principales sirven para reducir la dimensionalidad capturando la mayor varianza de los datos, se seleccionan matricialmente las componentes de mayor a menor contribución a la variabilidad de los datos. Si transformamos la matriz X = UdV donde U’U = V’V = I son los vectores singulares y d es la matriz con los valores singulares ya podremos obtener una solución por mínimos cuadrados.

En la documentación indicada con anterioridad están descritos los algoritmos empleados para realizar este tipo de modelos. Principalmente se basan en la descomposición en valores singulares lo que garantiza que la ortonormalidad. Y en función de la matriz utilizada estaremos ante PCR o PLS. Si el modelo emplea la matriz X para la obtención de las componentes estamos ante PCR, si el modelo emplea la matriz YX estamos ante PLS y en PLS si tenemos sólo una variable dependiente tenemos PLS1 y si tenemos más de una variable dependiente tendremos PLS2. Para conocer mejor los algoritmos que emplean estas técnicas recomiendo esta lectura.

Nuestro trabajo con R se va a centrar en PCR y PLS1. La librería que vamos a emplear para la realización de esta tarea en R será pls. Utilizamos los mismos datos que empleamos cuando trabajamos con la regresión ridge. Comenzamos nuestro trabajo con R:

url <- "http://www-stat.stanford.edu/~tibs/ElemStatLearn/datasets/prostate.data"
cancer <- read.table(url, header=TRUE)

entreno = subset(cancer,train=="TRUE")
entreno = entreno[,-10]
#install.packages("pls")
library(pls)

Descargamos los datos de una url y creamos el objeto cancer. Disponemos de una variable que nos permite distinguir los datos de entrenamiento de los datos de test. Nuestra variable dependiente de nuevo será el logaritmo de psa, del nivel del antígeno prostático. El primer modelo que vamos a realizar será la regresión por componentes principales, con el paquete pls esta tarea se lleva a cabo con la función pcr:

modelo_pcr <- pcr(lpsa~. , ncomp=8, data=entreno, validation="LOO")
summary(modelo_pcr)

Creamos un modelo con el número máximo de componentes 8 y realizamos una validación cruzada con el método LOO leave-one-out, dejando uno fuera. Típico método de validación cuando usas cuatro observaciones guarras. Por defecto pls tiene CV como método de validación, que realiza una validación cruzada más simple, también podemos emplear la opción none si no deseamos que se realice. Lo que es evidente es que necesitamos determinar el número más apropiado, por favor no emplear el término óptimo, de componentes. Vamos a graficar la raíz del cuadrado de los errores para determinar que número de componentes seleccionamos:

plot(RMSEP(modelo_pcr), legendpos = "topright",
main="Raiz del error para el modelo con PCR")

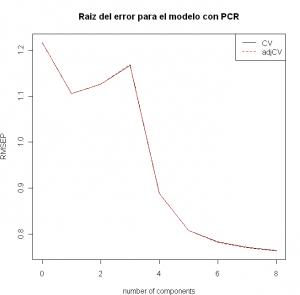Parece que 5 componentes pueden ser adecuados, aunque se sigue produciendo un descenso en la raíz del error pero en menor medida. Con estas matizaciones nuestro modelo final quedaría:

modelo_pcr <- pcr(lpsa~. , ncomp=5, data=entreno, validation="none")

Analizamos su comportamiento predictor:

test = subset(cancer,train=="FALSE")
test = test[,-10]

pred_pcr = predict(modelo_pcr,ncomp=5,newdata=test)
sum((test$lpsa-pred_pcr)^2)

La suma del cuadrado del error es 16.8 no es un modelo que mejore a un modelo de regresión por mínimos cuadrados ordinarios. En cualquier caso se recomienda tipificar las variables a la hora de realizar el modelo. Por defecto los algoritmos que incluye el paquete pls corrigen los datos por la media, pero si añadimos la opción sclale=TRUE además de corregir por la media dividiremos por la desviación típica:

modelo_pcr2 <- pcr(lpsa~. , ncomp=5, data=entreno, validation="none",scale=T)

pred_pcr2 <- predict(modelo_pcr2,ncomp=5,newdata=test)

sum((test$lpsa-pred_pcr2)^2)

La suma del cuadrado de los errores queda en 16.2 mejorando ligeramente el resultado anterior pero sin mejorar el resultado de mínimos cuadrados ordinarios. Evaluemos ahora el modelo PLS con los mismos datos:

modelo_pls = plsr(lpsa~. , ncomp=8, data=entreno, validation="LOO", scale=T)
summary(modelo_pls)
plot(RMSEP(modelo_pls), legendpos = "topright",
main="Raiz del error para el modelo con PLS")

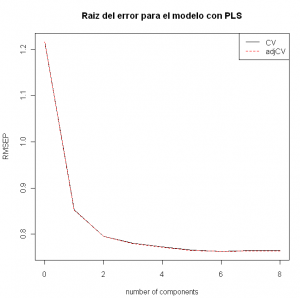
En este caso 4 componentes si parecen suficientes para realizar nuestro modelo ya que vemos que un mayor número no implica una sustancial mejora. Ajustemos el modelo con esas 4 componentes y comparemos con el modelo por componentes principales:

modelo_pls = plsr(lpsa~. , ncomp=4, data=entreno, validation="LOO",scale=T)
pred_pls = predict(modelo_pls,ncomp=4,newdata=test)
sum((test$lpsa-pred_pls)^2)

La suma de cuadrados del error está en 15 el modelo mejora al anterior pero no mejora a los resultados del modelo por regresión ridge. Es posible que nos interese analizar el comportamiento de los parámetros que obtenemos con el modelo. Para ello el paquete pls nos permite graficar los parámetros de la regresión en función del número de componentes:

plot(modelo_pls,legendpos="bottomleft", plottype='coef', 
labels=names(entreno), ncomp=1:4)

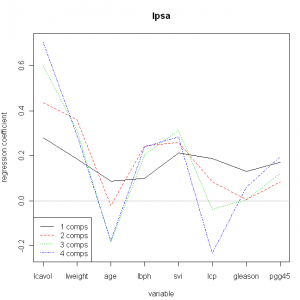
Vemos como la primera componente tiene unos parámetros del modelo muy similares para las variables, la segunda ya comienza a diferenciar el comportamiento de algunas variables y la tercera y la cuarta si producen mayores diferencias entre parámetros. Realicemos un gráfico de correlaciones de las cargas entre estas dos primeras componentes:

 plot(modelo_pls,plottype="correlation", labels=names(entreno))

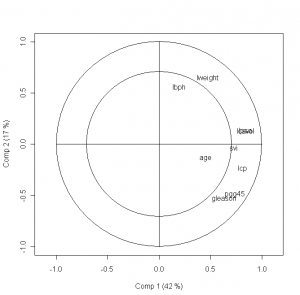
Las cargas y las puntuaciones son los dos elementos más útiles a la hora de realizar interpretaciones sobre los parámetros de nuestro modelo. Provienen del algoritmo que se utiliza para obtener los parámetros del modelo. Probablemente el análisis de cargas tenga una entrada propia. Saludos.