Regresión ridge o regresión contraída con R

Por lo visto no he estudiado lo suficiente. Tengo que redimirme y estudiar este verano determinadas técnicas avanzadas de predicción. Fundamentalmente tengo que trabajar con R y tener determinados conocimientos teóricos sobre estas técnicas. Así que he pensado que, a la vez que estudio yo, estudian todos mis lectores. Además es probable que genere debate.

En esta primera entrega vamos a tratar la regresión contraída o regresión ridge. En el blog ya hablamos del problema que suponía la multicolinealidad  cuando tenemos este problema una de las posibles soluciones es la regresión contraída o regresión ridge. Como ya dijimos el modelo lineal se expresa como Y = X • Beta + Error la estimación de nuestros parámetros Beta por mínimos cuadrados ordinarios es Beta = inv(X’X) * X’Y cuando X’X no es invertible tenemos un problema. La regresión ridge plantea una solución a este problema con unos parámetros Beta_contraidos =  inv(X’X + lambda*I) * X’Y si lambda es 0 estamos ante mínimos cuadrados ordinarios, en otro caso estamos ante un estimador sesgado de Beta. Este estimador sesgado es solución al problema de mínimos cuadrados penalizados y lo que hace es contraer los Betas en torno a 0. En resumen, metemos sesgo pero reducimos varianza.

Para llevar a buen puerto esta técnica el talento reside en encontrar ese lambda que contrae mis estimaciones. Para encontrarlo se utiliza un criterio generalizado de validación cruzada, generalized cross-validation (GCV). El proceso fija un rango de posibles lambda entre [0, c] y calcula la validación cruzada CV. El lambda óptimo es aquel que minimiza el CV. Con él podemos obtener la solución a los mínimos cuadrados contraídos.

En cuanto al trabajo con R vamos a emplear documentación que podéis encontrar aquí:

http://www-stat.stanford.edu/~tibs/ElemStatLearn/

# The following dataset is from Hastie, Tibshirani and Friedman (2009), from a study
# by Stamey et al. (1989) of prostate cancer, measuring the correlation between the level
# of a prostate-specific antigen and some covariates. The covariates are
#
# * lcavol  : log-cancer volume
# * lweight : log-prostate weight
# * age     : age of patient
# * lbhp    : log-amount of benign hyperplasia
# * svi     : seminal vesicle invasion
# * lcp     : log-capsular penetration
# * gleason : Gleason Score, check http://en.wikipedia.org/wiki/Gleason_Grading_System
# * pgg45   : percent of Gleason scores 4 or 5
#
# And lpsa is the response variable, log-psa.

url <- "http://www-stat.stanford.edu/~tibs/ElemStatLearn/datasets/prostate.data"
cancer <- read.table(url, header=TRUE)
str(cancer)

install.packages("car")
library(car)
library(MASS)

entreno = subset(cancer,train=="TRUE")
modelo_mco <- lm(lpsa~ . , data=entreno[,-10])
summary(modelo_mco)

Disponemos del data frame cáncer que tiene 10 variables y 97 observaciones y se empleó en un estudio para determinar que variables influyen en la presencia de un antígeno prostático específico para detectar el cáncer de próstata. Disponemos de una variable que nos distingue el entrenamiento del test. Lo primero es elaborar un modelo por mínimos cuadrados ordinarios. El estadístico F es muy próximo a 0 luego tenemos modelo, un R2 de 0,65 es aceptable pero sólo 2 variables aparecen como significativas a un nivel de 0,1. Podemos sospechar la existencia de problemas con X’X. En este caso no es un ejemplo “de libro”. He pretendido que sólo haya una sospecha de multicolinealidad, me ha costado encontrar unos datos que hicieran esto. La sospecha multicolinealidad se puede analizar con el VIF que obtenemos con la función vif de la librería car:

 vif(modelo_mco)
  lcavol  lweight      age     lbph      svi      lcp  gleason    pgg45 
2.318496 1.472295 1.356604 1.383429 2.045313 3.117451 2.644480 3.313288

Tenemos 2 valores por encima de 3. ¿De verdad es necesario introducir un sesgo? Vamos a realizar el modelo de regresión contraída para encontrar ese sesgo que me reduzca la varianza:

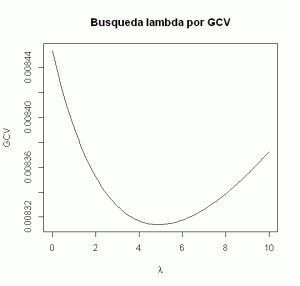
modelo_contraida <- lm.ridge(lpsa ~ ., data=entreno[,-10], lambda = seq(0,10,0.1))

plot(seq(0,10,0.1), modelo_contraida$GCV, main="Busqueda lambda por GCV", type="l",
     xlab=expression(lambda), ylab="GCV")

Vemos que el lambda ha de estar muy próximo a 5 para saber el valor óptimo empleamos la función select:

select(lm.ridge(lpsa ~ ., data=entreno[,-10], lambda = seq(0,10,0.1)))
modified HKB estimator is 3.355691 
modified L-W estimator is 3.050708 
smallest value of GCV  at 4.9

El valor que minimiza el GCV es 4.9 ya estamos en disposición de crear el modelo. Si deseamos ver gráficamente como se modifican los parámetros de nuestro modelo en función de lambda podemos realizar lo siguiente:

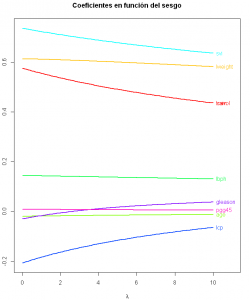
matplot(seq(0,10,0.1), coef(modelo_contraida)[,-1], xlim=c(0,11), type="l",xlab=expression(lambda), 
        ylab=expression(hat(beta)), col=colors, lty=1, lwd=2, main="Coeficientes en función del sesgo")

text(rep(10, 9), coef(modelo_contraida)[length(seq(0,10,0.1)),-1], colnames(entreno)[-9], 
     pos=4, col=colors)

Observamos como los parámetros del modelo van siendo cada vez más “estrechos”, se van contrayendo. Insistimos, estamos introduciendo un sesgo para tener menos varianza. Pero volvamos a la cuestión anterior ¿De verdad es necesario introducir este sesgo? Comparemos con los datos de validación el modelo obtenido por mínimos cuadrados ordinarios con el modelo obtenido por regresión ridge con los datos de test:

ajuste_mco <- predict(modelo_mco,test)
sum((test$lpsa-ajuste_mco)^2)

Para el modelo por mínimos cuadrados obtenemos una suma de cuadrados del error de 15,7 para los datos ajustados del conjunto de datos de test. Realizamos el mismo proceso para el modelo con regresión ridge. Pero en este caso es necesario realizar cálculo matricial porque mediante el paquete car no nos funciona predict.

#Modelo con lambda optimo
modelo_contraida <- lm.ridge(lpsa ~ ., data=entreno[,-10], lambda = 4.9)
#estos objetos no admiten predict
coeficientes <- as.vector(coef(modelo_contraida))
matriz <- as.matrix(test[,-9])
matriz <- cbind(rep(1,length=nrow(test)),matriz)
ajuste_contraida <- matriz %*% coeficientes
sum((test$lpsa- ajuste_contraida)^2)

Para esta validación lo primero es obtener el modelo con el lambda óptimo que obtuvimos con la función select anteriormente. Extraemos los coeficientes del modelo y los introducimos en un vector. Los datos de test a su vez los metemos en una matriz, pero es necesario tener una columna inicial en la matriz con unos para el término independiente del modelo. Multiplicamos la matriz de datos por el vector de coeficientes y tenemos los datos ajustados para la regresión ridge. Ya estamos en disposición de ver el cuadrado de la diferencia entre los datos ajustados y los datos reales. El resultado final es 14,8 luego el modelo ajusta mejor que el realizado por mínimos cuadrados.