Retomamos un asunto tratado en días anteriores, los peligros de realizar un análisis de agrupamiento basado en las distancias entre observaciones. ¿Cómo podemos evitar este problema? Empleando máquinas de vectores de soporte, traducción de Support Vector Machines (SVM). Esta técnica de clasificación de la que ya hablamos en otra entrada nos permite separar observaciones en base la creación de hiperplanos que las separan. Una función kernel será la que nos permita crear estos hiperplanos, en el caso que nos ocupa tenemos sólo dos variables, necesitamos crear líneas de separación entre observaciones. En la red tenéis una gran cantidad de artículos sobre estas técnicas.
Para ilustrar como funciona retomamos el ejemplo anterior:
#GRUPO 1
x = runif(500,70,90)
y = runif(500,70,90)
grupo1 = data.frame(cbind(x,y))
grupo1$grupo = 1
#GRUPO 2
x = runif(1000,10,40)
y = runif(1000,10,40)
grupo2 = data.frame(cbind(x,y))
grupo2$grupo = 2
#GRUPO 3
x = runif(3000,0,100)
y = runif(3000,0,100)
grupo3.1 = data.frame(cbind(x,y))
grupo3.1separacion=(x+y)
grupo3.1 = subset(grupo3.1,separacion>=80&separacion <=140,select=-separacion)
grupo3.1 = subset(grupo3.1,y>0)
grupo3.1grupo = 3
#UNIMOS TODOS LOS GRUPOS
total=rbind(grupo1,grupo2,grupo3.1)
plot(totalx,totaly,col=c(1,2,3)[total$grupo])
El paquete de R que vamos a emplear es kernlab, vamos a separar nuestro conjunto de datos en entrenamiento para el algoritmo y posteriormente clasificaremos:
#install.packages("kernlab")
#Creamos un conjunto de entrenamiento y validación
elimina = sample(1:nrow(total),1000)
clasifica = total[elimina,]
entrena = total[-elimina,]
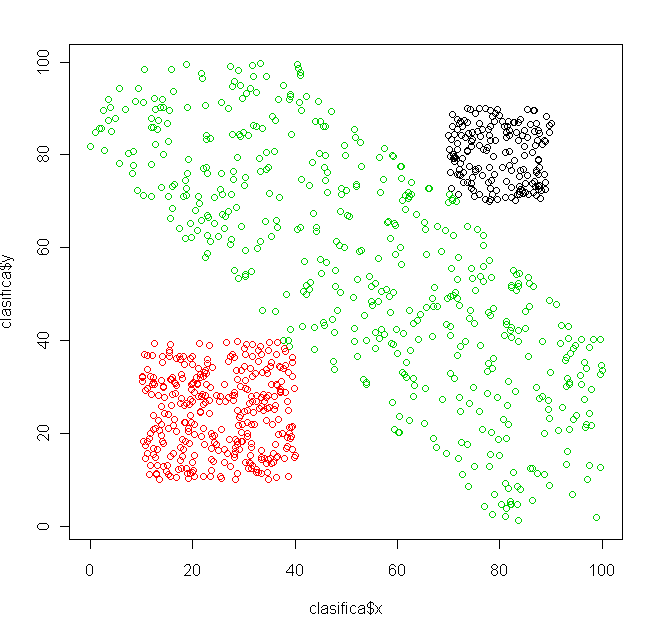
Ahora vamos a emplear el algoritmo con la función ksvm y analizamos los resultados sobre el objeto clasifica:
library(kernlab)
modelo predic = data.frame(predict(modelo,clasifica ))
clasifica = cbind(clasifica,predic=predic)
plot(clasificax,clasificay,col=c(1,2,3)[clasifica$predict.modelo..clasifica.])
En type especificamos el tipo de análisis a realizar, en este caso C-svc es una clasificación, podemos hacer regresiones y algún día volveré sobre ello. La función kernel para separar las observacioes es vanilladot; es la función lineal, la más apropiada en este caso, pero tenéis entre otras:
–polydot kernel polinómico
–tanhdot tangent hiperbólica
–splinedot basada en splines
El funcionamiento no puede ser mejor:
Esto contrasta con los resultados obtenidos mediante distancias. Tened siempre en mente el uso de esta técnica para clasificar, no os centréis sólo en el análisis cluster o discriminante. Esta técnica tiene mucho recorrido sobre todo en biología. Saludos.