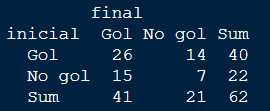«Suponiendo que los lanzamientos de una tanda de penaltis son independientes…» Así empiezo parte de una formación que imparto y siempre he pensado que no tiene ningún sustento científico y se me ha ocurrido estudiar la validez de esta suposición. Y por ello vamos a emplear datos de Statsbomb para investigar si un lanzamiento de una tanda de penaltis es independientes del anterior y aprovechamos para conocer el test de la chi cuadrado
¿Qué es un suceso/penalti independiente? Un penalti es independiente del otro si la probabilidad de uno no influye sobre la probabilidad del otro, es decir, un lanzamiento no depende del resultado de los anteriores. Para estudiar si una sucesión de números es independiente existen test estadísticos pero en el párrafo anterior ya se desvela lo que vamos a analizar, ¿un lanzamiento es independiente del anterior?. El problema lo podemos hacer tan complejo como queramos y ver la tanda de 5 penaltis en su conjunto, trabajar con funciones del paquete randomizeR, hacer test de independencia de vectores aleatorios, emplear test de estadísticos con nombres impronunciables,… Pero, ¿no será más sencillo estudiar si el resultado de un penalti depende del anterior? Este ejercicio quiero que sirva también para reflexionar sobre la complejidad de los contrastes de hipótesis.
Para este ejemplo vamos a emplear StatsBombR y los datos de eventos de competiciones de acceso gratuito:
library(tidyverse)
library(StatsBombR)
comp <- FreeCompetitions()
De las competiciones gratuitas seleccionamos el mundial de Qatar (datos gratuitos recientes) y el mundial de «cuando caía bien Rusia». Se pueden usar más competiciones, pero en este momento estoy en la Siberia Extremeña y estoy conectado a un móvil situado en la ventana con mejor cobertura, tened en cuenta que nos estamos descargando datos de eventos y son miles de registros.
partidos <- FreeMatches(FreeCompetitions()) %>%
filter(season.season_id %in% c(106,3) & competition_stage.name != 'Group Stage')
eventos <- StatsBombFreeEvents(MatchesDF = partidos)
tandas_penalties <- eventos %>% filter(period>=5 & type.name=='Shot')
Entre los partidos también han sido eliminados los de fase de grupos (no hay tandas) y algo que no sabía, Statsbomb interpreta que la tanda de penaltis es el quinto periodo, por si acaso, sólo nos quedamos con los tiros. En este punto tenemos 80 lanzamientos de penalti. Ya hemos comentado que se puede sofisticar mucho el análisis pero no hay necesidad, estamos ante datos binomiales y vamos a poner el resultado del lanzamiento inicial y el resultado del lanzamiento siguiente.
tandas_penalties <- tandas_penalties %>%
arrange(match_id, team.id, index) %>%
group_by(match_id, team.id) %>%
mutate(orden = row_number()) %>%
as_tibble()
table(tandas_penalties$orden)
Se crea una variable orden del lanzamiento en la tanda como resultado de ordenar por partido, equipo e índice de la jugada. Un apunte, me ha llamado la atención que no se llega a un sexto lanzamiento e incluso que pocas veces se llega al quinto. No he buscado en prensa si se alargó alguna tanda pero me ha resultado extraño. Hecho el apunte, de forma muy sencilla obtenemos cada lanzamiento por orden para posteriormente unir los datos. No se complica el código con bucles sofisticados.
uno <- tandas_penalties %>% filter(orden==1) %>% select(match_id, team.id, shot.outcome.name)
dos <- tandas_penalties %>% filter(orden==2) %>% select(match_id, team.id, shot.outcome.name)
tres <- tandas_penalties %>% filter(orden==3) %>% select(match_id, team.id, shot.outcome.name)
cuatro <- tandas_penalties %>% filter(orden==4) %>% select(match_id, team.id, shot.outcome.name)
cinco <- tandas_penalties %>% filter(orden==5) %>% select(match_id, team.id, shot.outcome.name)
Ahora se une el inicial con el siguiente elaborando unos datos homogéneos.
uno <- uno %>% left_join(dos, by = c("match_id", "team.id")) %>%
rename(inicial = shot.outcome.name.x, final = shot.outcome.name.y)
dos <- dos %>% left_join(tres, by = c("match_id", "team.id")) %>%
rename(inicial = shot.outcome.name.x, final = shot.outcome.name.y)
tres <- tres %>% left_join(cuatro, by = c("match_id", "team.id")) %>%
rename(inicial = shot.outcome.name.x, final = shot.outcome.name.y)
cuatro <- cuatro %>% left_join(cinco, by = c("match_id", "team.id")) %>%
rename(inicial = shot.outcome.name.x, final = shot.outcome.name.y)
Cuatro conjuntos de datos con la misma estructura se unen horizontalmente y resumimos el resultado en Gol-No gol.
df <- rbind.data.frame(uno, dos, tres, cuatro) %>%
mutate(inicial = ifelse(inicial == "Goal", "Gol", "No gol"),
final = ifelse(final == "Goal", "Gol", "No gol")) %>%
filter(!is.na(final))
remove(uno, dos, tres, cuatro, cinco)
Ya estamos en disposición de medir si el lanzamiento es independiente del anterior. Al tratarse de dos variables binomiales (Gol/No gol) se va a optar por emplear el test estadístico más conocido como es el test de la Chi-cuadrado que determina si dos variables cualitativas son independientes. Es un test que emplea la tabla de frecuencias para establecer si la diferencia entre lo observado y lo que se espera es estadísticamente significativa. La tabla de frecuencias con los datos es.
tabla <- df %>% group_by(inicial,final) %>% summarise(tiros = n())
xtabs(tiros ~ inicial + final, data = tabla) %>% addmargins()
Se intuye la independencia, sin embargo, para corroborar la validez estadística de nuestras impresiones vamos a emplear el test de la chi-cuadrado. Este test paramétrico (viejuno) mide lo que esperamos menos lo que sale, y qué esperamos si inicialmente tenemos un gol y luego vuelve a ser gol, pues esperamos el producto de los totales entre el total de observaciones, en el caso de gol y gol (40*41)/62= 27.8 y nos sale 26 y siempre elevamos al cuadrado para evitar el efecto signo por lo que lo observado – lo esperado = 3.14 y haciendo esta fórmula \chi^2 = \sum_{k=1}^n {(O_i-E_i)^2 \over E_i} se obtiene el estadístico asociado al test. Ese estadístico sigue una distribución n-1 niveles del factor inicial, en este caso 1 porque sólo hay dos posibles resultados y m-1 niveles del factor inicial, de nuevo 1. Pero vamos, en R hacemos.
chisq.test(dfinicial,dffinal)
El test de la chi cuadrado contrasta una hipótesis inicial de independencia, casi todos los test viejunos contrastan siempre una igualdad, igualdad de medias, independencia,… El caso es que la probabilidad asociada a ese estadístico es 1 así que es mejor no rechazar la hipótesis nula y hay una independencia entre el primer lanzamiento y el segundo.
Parece que puedo seguir diciendo: «Suponiendo que los lanzamientos de una tanda de penaltis son independientes…»
Siento no poder ilustrar un análisis de independencia de vectores binomiales, perdí un poco la cabeza