El modelo multivariante en el sector asegurador. La variable dependiente (III)

Hasta ahora estamos hablando de un concepto muy difuso que denomino comportamiento siniestral. A la hora de ajustar un modelo estadístico necesito una variable dependiente que será función de otras variables independientes. Las variables independientes serán los riesgos a los que también les dedicaremos unas líneas, y la variable independiente será el comportamiento siniestral; pero este concepto un poco difuso no lo vamos a medir en una sóla variable si no en dos:

• Número de siniestros que en función de la exposición nos determina la frecuencia siniestral

• Coste de los siniestros que nos determina el coste medio de los siniestros

Esto conlleva la necesidad de ajustar al menos 2 modelos. También se pueden definir distintos tipos de siniestros y se ajustarán los modelos que consideremos para cada tipo de siniestro (imaginemos pagos por módulos o acuerdos entre compañías), también es muy interesante distinguir siniestros materiales y corporales, cada tipo de siniestro tendría su correspondiente modelo de frecuencia y costes medios. Al final a cada resultado le asignamos una ponderación y con ello obtendríamos una estructura tarifaria como resultado de varios modelos. Pero en este acercamiento consideramos que todos los siniestros son iguales por lo que tenemos que ajustar dos modelos: uno de frecuencias y otro de costes medios.

Como en todos los procesos de modelización el primer paso es conocer como se distribuyen nuestras variables dependientes a lo largo del tiempo,  el numero de siniestros en función de los clientes tiene una forma parecida a esta:

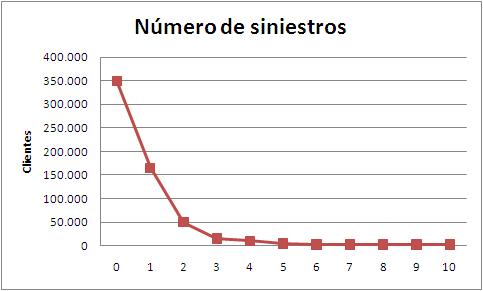
Afortunadamente para las aseguradoras son menos los clientes que tienen siniestros que aquellos que tienen más de un siniestro. Si pasamos por ICEA la frecuencia se situa en torno a un 35% de la exposición. Parece que su distribución se ajusta a una exponencial. Los costes medios los representamos en barras:

En el caso de los costes tenemos una situación muy parecida a la anterior, este ejemplo se representan tramos de costes (eje x) frente a costes totales (eje y). La distribución es muy similar a la exponencial con la salvedad de la cola de la derecha que agrupa un alto % del importe de la siniestralidad. Sería necesario realizar un corte para que esos siniestros no participaran en el modelo de costes medios. En nuestro caso el corte puede estar en torno a los 200.000 – 300.000 euros. Es una forma de eliminar registros que pueden falsear la estimación.

Estas serán nuestras variables dependientes en el multivariante. Ajustaremos dos modelos, un modelo para las frecuencias y otro modelo para los costes medios. Por cierto, cualquier parecido con la realidad de los graficos aqui presentados es pura coincidencia.