Cuando tenemos que evaluar el comportamiento de un modelo de clasificación binomial empleamos sensibilidad, especificidad,… ya he hablado sobre ese tema aunque volveré sobre ello. Sin embargo, si nuestro modelo estima un valor es posible que no tengamos tan claro como está funcionando su capacidad predictiva. Lo que traigo hoy es un análisis muy básico pero que entienden muy bien aquellas personas que no tienen grandes conocimientos en ciencia de datos, además es una continuación de la entrada en la que se ilustraba un ejemplo de uso de los modelos tweedie.
Una vez ejecutado el proceso que realizaba el modelo tweedie disponíamos de un objeto norauto con las variable prima_estimada que era el resultado de la estimación de nuestro modelo tweedie sobre la prima pura de la cartera de automóviles con la que estamos trabajando. ¿Esa estimación es buena? ¿Cómo sé si es buena? Para medir la capacidad predictiva propongo contrastar la estimación frente al azar, lo que se llama «ganancia».
Con los datos resultantes del modelo tweedie podemos hacer lo siguiente.
library(formattable) norauto <- norauto %>% mutate(numero_aleatorio = runif(nrow(norauto))) grupos = 10 norauto <- norauto %>% arrange(numero_aleatorio) %>% mutate(tramos= as.factor(ceiling((row_number()/n())*grupos))) resumen_aleatorio <- norauto %>% group_by(tramos=tramos_aleatorios) %>% summarise(porcen_aleatorio = sum(ClaimAmount)/sum(norauto$ClaimAmount)) format_table(resumen_aleatorio)
| tramos | porcen_aleatorio |
|---|---|
| 1 | 0.10556040 |
| 2 | 0.09958607 |
| 3 | 0.08824017 |
| 4 | 0.10940522 |
| 5 | 0.10914120 |
| 6 | 0.08647070 |
| 7 | 0.09336329 |
| 8 | 0.10933129 |
| 9 | 0.09408481 |
| 10 | 0.10481685 |
Si repasamos los porcentajes del reparto aleatorio están muy cerca del 10%, si dividimos al azar en 10 grupos cabe esperar que cada grupo entre tenga un 10% de siniestralidad, sencillo. Si en vez de ordenar por un número al azar ordenamos de mayor a menor por la prima pura estimada con un proceso análogo al anterior.
norauto <- norauto %>% arrange(desc(prima_estimada)) %>% mutate(tramos_estimados= as.factor(ceiling((row_number()/n())*grupos))) resumen_estimacion <- norauto %>% group_by(tramos=tramos_estimados) %>% summarise(porcen_estimado = sum(ClaimAmount)/sum(norauto$ClaimAmount)) format_table(resumen_estimacion)
| tramos | porcen_estimado |
|---|---|
| 1 | 0.25826315 |
| 2 | 0.15391311 |
| 3 | 0.14599617 |
| 4 | 0.11960301 |
| 5 | 0.08425770 |
| 6 | 0.07620388 |
| 7 | 0.05097079 |
| 8 | 0.04654863 |
| 9 | 0.04147418 |
| 10 | 0.02276937 |
En el grupo con mayor prima pura esperada se concentra el 26% de la siniestralidad real, en el grupo con menor prima pura esperada se concentra el 2% de la siniestralidad real. ¿Cuánto estamos ganando? En el primer tramo mejoramos en 2.6 veces al azar, si acumulamos tramos con 2 ya estamos cogiendo más del 40% de la siniestraldiad, gráficamente.
left_join(resumen_aleatorio, resumen_estimacion) %>% mutate(porcen_aleatorio = cumsum(porcen_aleatorio),
porcen_estimado = cumsum(porcen_estimado)) %>%
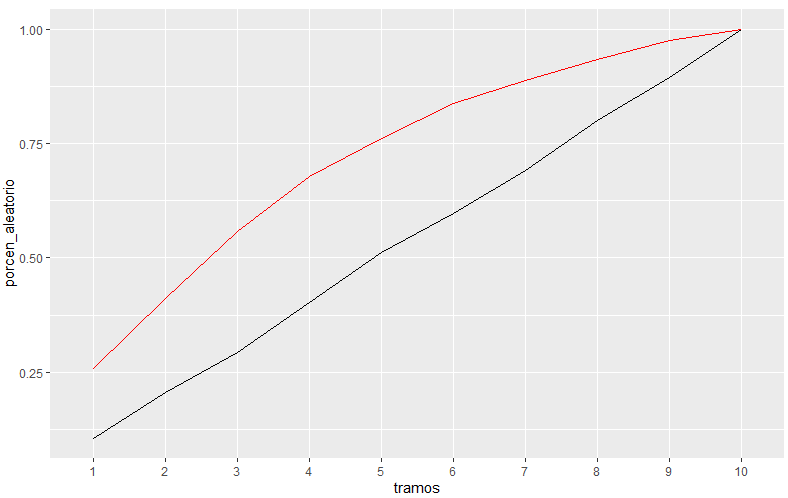
ggplot(aes(x=tramos, y=porcen_aleatorio, group=1)) + geom_line() +
geom_line(aes(x=tramos, y=porcen_estimado),color='red')
Se aprecia como el modelo va superando al azar, con un 50% de las observaciones tenemos a nuestro alcance el 75% de la siniestralidad. Ahora queda a juicio del gestor de estos datos y de las personas implicadas en su uso si es suficientemente bueno.