Os propongo un juego con R. El juego parte de unos datos aleatorios que he generado con R (los que veis arriba) que dividimos en entrenamiento y test. Sobre el conjunto de datos de entrenamiento he realizado varios modelos y valoro las predicciones gráficamente sobre los datos de test. El juego consiste en asociar cada resultado gráfico de test a cada código de R correspondiente y justificar brevemente la respuesta.
Los gráficos de los datos de test son:
Los códigos R que tenéis que asociar a cada figura son:
Código 1: Red neuronal con una sólo capa y 2 nodos:
mejor.red {
mejor.rss for(i in 1:50){
modelo.rn linout=T, trace=F,decay=0.1)
if(modelo.rn$value < mejor.rss){
mejor.modelo mejor.rss
return(mejor.modelo)
}}
}
mejor.red(2)
Código 2: Regresión lineal
lm(dep ~ indep,entrenamiento)
Código 3: Máquina de vector de soporte con un margen muy alto
svm(dep ~ indep ,entrenamiento, method=»C-classification»,
kernel=»radial»,cost=100,gamma=100)
Código 4: Árbol de regresión
rpart(dep~indep,entrenamiento)
Código 5: Regresión LOESS
loess (dep ~ indep, data = entrenamiento)
Código 6: Máquina de vector de soporte con un margen bajo
svm(dep ~ indep ,entrenamiento, method=»C-classification»,
kernel=»radial»,cost=10,gamma=10)
Código 7: K vecinos más cercanos K-nn
train.kknn(dep ~ indep, data = entrenamiento,
k = 4, kernel = c(«rectangular»))
Por ejemplo la figura A irá con el código 2 porque se trata de una estimación lineal. Y ahora os toca a vosotros asociar figuras a modelos de R.
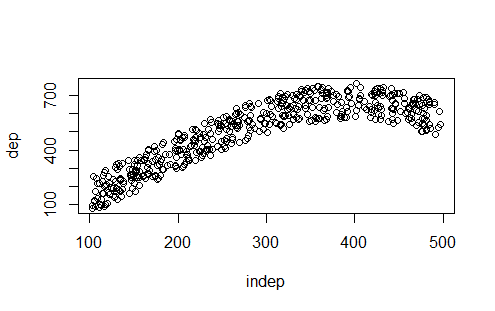
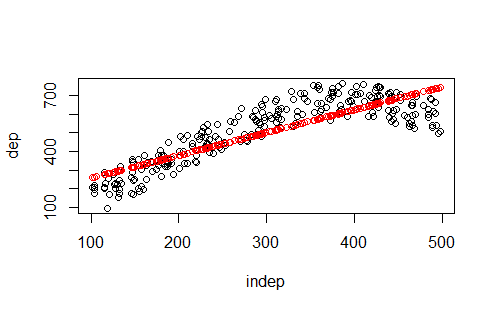
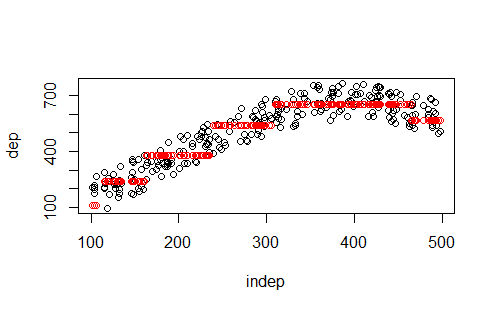
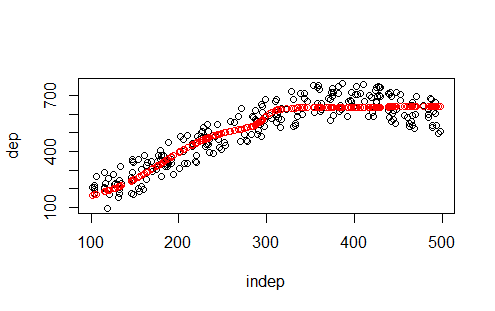
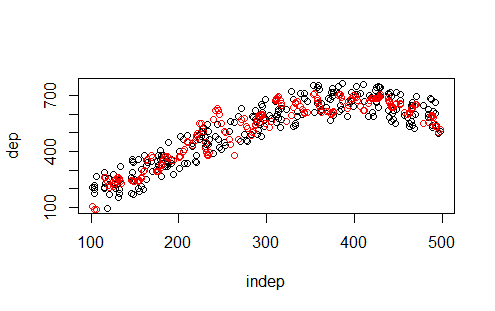
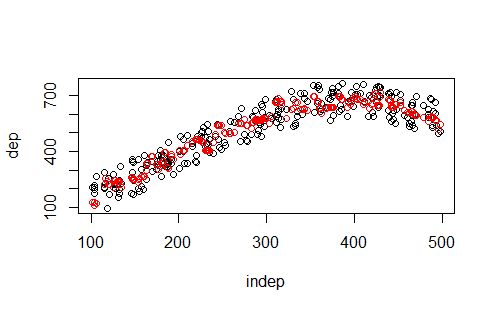
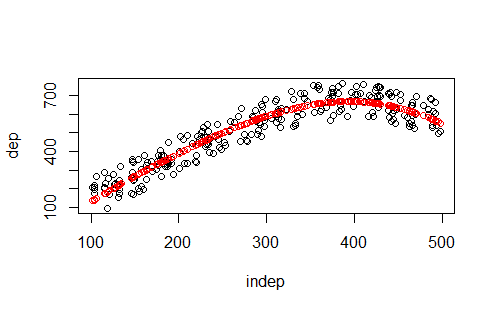

Figura B código 4 ?
Efectivamente pinta una estimación escalonada. Muy sencillo. Esta es fácil, pero ¿cómo salva la linealidad una red neuronal? ¿Cómo distingues el knn del SVM con poco margen?
Pues si. Complicadillo, yo diría que el knn es la figura D
K-nn no te clasifica ninguna observación que no esté cerca de los datos por su propia definición. Las bolas rojas tienen que estár rodeadas de bolas negras y no tener una tendencia.
Pingback: Resolución del juego de modelos con R | Análisis y Decisión