En la temporada 22/23 de la Liga el RCD Espanyol descendió a segunda división y los aficionados culpamos en parte los problemas que hubo durante toda la temporada con los porteros y quería analizar si hubo diferencias entre los porteros que jugaron esa temporada en el Espanyol y Diego López que jugó como portero titular la temporada anterior, dejaremos de lado las intervenciones de Joan García y Olazábal.
Comenzamos con un código conocido.
library(worldfootballR)
library(tidyverse)
# Toda la información la extraemos de FBRef
# Extraemos los partidos
partidos <- data.frame(url=fb_match_urls(country = "ESP", gender = "M",
season_end_year = c(2022,2023), tier = "1st"))
En los parámetros de las funciones de fb_* podemos poner listas, de ese modo nos descargamos 2 temporadas. Y ahora es necesario quedarnos sólo con los partidos del Espanyol.
partidos <- partidos %>% filter(grepl("Espanyol",url) >0 )
Filtrados los partidos del Espanyol nos bajamos las alineaciones, paciencia con este proceso, son muchos partidos.
alineaciones <- tibble()
for (i in seq(1:nrow(partidos))) {
ax <- fb_match_lineups(partidos[i,1])
alineaciones <- rbind.data.frame(alineaciones, ax)
}
Replicamos un código anterior para determinar los partidos del Espanyol. Si alguien tiene una mejor forma de hacerlo es bienvenida.
alineaciones <- alineaciones %>% mutate(local =substr(MatchURL,30, length(MatchURL)),
local = substr(local, str_locate(local, "/")[,1]+1, length(MatchURL)),
local = str_replace(local,'El-Derbi-Madrileno-',''),
local = str_replace(local, 'El-Clasico-',''))
alineaciones <- alineaciones %>%
mutate(equipo = case_when(
substr(local,1,8)=='Espanyol' & Home_Away=='Home' ~ "Espanyol",
substr(local,1,8) != 'Espanyol' & Home_Away=='Away' ~ "Espanyol",
TRUE ~ 'Rival' ))
alineaciones_Espanyol <- alineaciones %>% filter(equipo=="Espanyol")
porteros <- alineaciones_Espanyol %>% filter(Pos=='GK')
table(porteros$Player_Name)
Otro proceso largo, necesitamos todos los tiros de todos los partidos que estamos estudiando.
shots <- tibble()
for (i in seq(1:nrow(partidos))) {
ax <- fb_match_shooting(partidos[i,1])
shots <- rbind.data.frame(shots, ax)
}
Evidentemente sólo nos quedamos con los tiros que le hacen al Espanyol.
shots <- shots %>% filter(Squad != 'Espanyol')
Ahora de todos esos tiros que le hacen al Espanyol con una left join determinamos que portero estaba jugando en ese encuentro.
porteros <- alineaciones_Espanyol %>% filter(Pos=='GK') %>% select(Matchday, Player_Name)
elimina <- porteros %>% group_by(Matchday) %>% summarise(conteo=n()) %>%
filter(conteo>1)
porteros <- porteros %>% filter(!Matchday %in% elimina$Matchday) %>%
mutate(Matchday=as.character(Matchday))
shots_final <- shots %>% inner_join(porteros, by=c("Date"="Matchday"))
Eliminamos los penalties.
shots_final <- shots_final %>% filter(!grepl("(pen)",Player))
table(shots_finalPlayer_Name,shots_finalOutcome)
A continuación creamos una suma de tiros acumulada que se resetea cuando el Español encaja un gol, de ese modo se podrá determinar cuantos tiros le hacen al portero que jugaba en ese partido. Para ello empleamos la librería hutilscpp y la función cumsum_reset que sirve para realizar sumas acumuladas de valores booleanos.
library(hutilscpp)
shots_final <- shots_final %>%
mutate(result_shot=ifelse(Outcome=='Goal','Gol','No gol')) %>%
arrange(Date, Minute) %>%
# Si el tiro anterior es gol empieza como FALSE
mutate(NoGol = ifelse(lag(result_shot) == "Gol", FALSE, TRUE),
NoGol = ifelse(is.na(NoGol), TRUE, NoGol)) %>%
mutate(Tiros_Gol = cumsum_reset(NoGol)) %>%
filter(!Player_Name %in% c('Joan García', 'Oier Olazábal')) %>%
dplyr::select(-NoGol)
En este punto, disponemos de una variable Tiros_Gol que nos mide la racha de cada portero. Gráficamente podemos emplear gráficos de densidades.
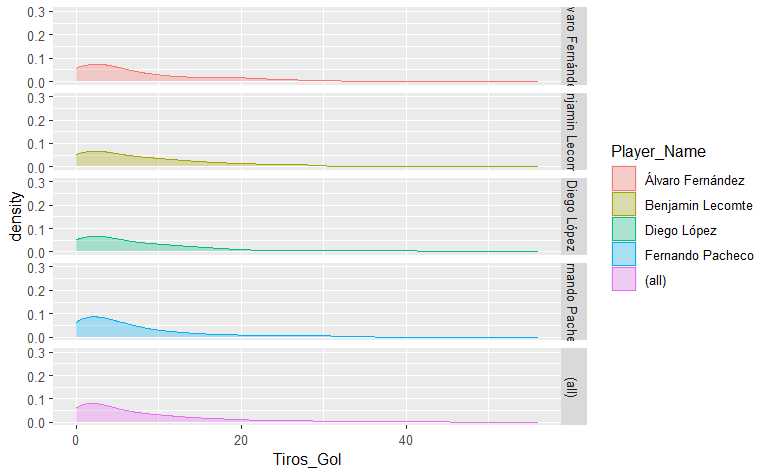
shots_final %>% ggplot(aes(Tiros_Gol, fill = Player_Name, color=Player_Name)) + geom_density(alpha=0.3) +
ylim(0, 0.3) +
facet_grid(Player_Name ~ ., margins = TRUE, scales = "free")
Se puede apreciar algún comportamiento negativo en Pacheco, no tan negativo en Lecomte y positivo en Diego López, pero nada que se pueda destacar. Si estudiamos algunos estadísticos de posición y dispersión
shots_final %>% group_by(Player_Name) %>% summarise(media = mean(Tiros_Gol),
p25 = quantile(Tiros_Gol,0.25),
meidana= median(Tiros_Gol),
p75 = quantile(Tiros_Gol,0.75),
desviacion=sd(Tiros_Gol))
Datos parecidos pero es Diego López el que tiene más variación, parece que mantuvo alguna racha más larga. Sin embargo, os propongo emplear una distribución discreta de probabilidad llamada Binomial Negativa que mide el número de casos hasta el éxito, en esta situación mide el número de tiros hasta el gol. Se considera cada tiro independiente del anterior (sé que es mucho suponer) y podemos hacer un modelo de regresión binomial negativa donde empleamos como variable dependiente Y el número de tiros hasta gol y como variable independiente el portero del Espanyol que estaba bajo palos, además, ponderamos los tiros por el xG que han generado de forma que también valoramos algo la acción defensiva.
library(MASS)
shots_final <- shots_final %>% mutate(xG = as.numeric(xG))
modelo <- glm.nb(Tiros_Gol ~ Player_Name + offset(xG), data=shots_final)
summary(modelo)
La librería MASS tiene la funcion glm.nb que permite hacer modelos de regresión binomial negativa, la sintaxis es muy sencilla y como se comentó con anterioridad el xG va a ponderar cada acción de tiro. Sumarizando el modelo se aprecia que sólo es significativo el parámetro asociado a Diego López, esto es, debido al bajo número de partidos que tenemos de Lecomte (y muchos fueron) y de Pacheco o debido a que tanto Lecomte, Fernández y Pacheco fueron igual de malos. Planteamos medir si existen diferencias entre Diego y los demás porteros.
shots_final <- shots_final %>% mutate(Portero = ifelse(Player_Name=='Diego López', 'Diego', 'Resto'))
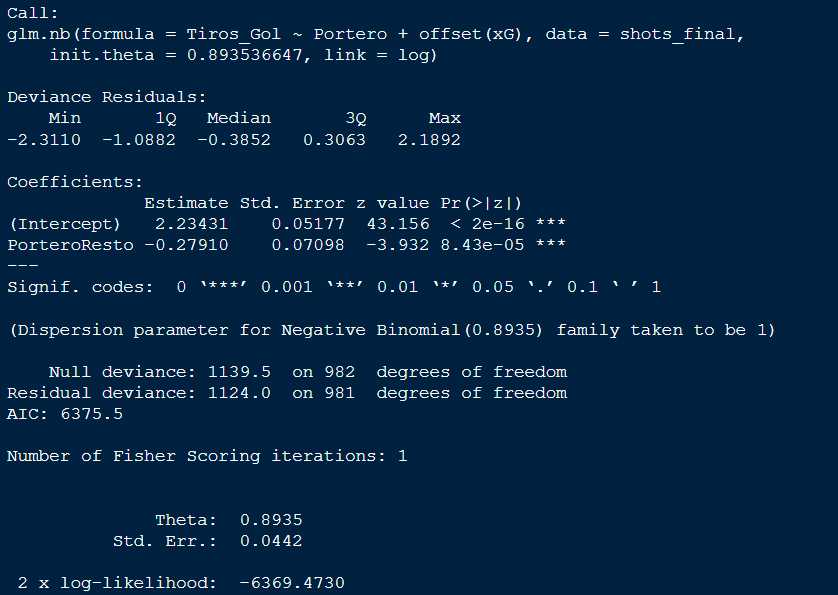
modelo2 <- glm.nb(Tiros_Gol ~ Portero + offset(xG), data=shots_final)
summary(modelo2)
En este segundo modelo el parámetro asociado al portero si tiene una validez estadística, el p-valor asociado al contraste de hipótesis «el parámetro suma 0» es muy próximo a 0 luego son distintas las rachas de tiros hasta gol entre Diego López y los porteros de la temporada 22/23.
Ahora interpretemos los resultados del modelo. Al igual que la regresión de poisson se trata de un modelo lineal generalizado cuya función de enlace es logarítmica por lo que haciendo el exponencial de los parámetros facilitaremos la interpretación como «efectos multiplicativos». Haciendo el exponencial de los parámetros tenemos.
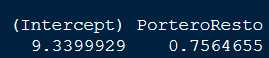
exp(modelo2$coefficients)
Estos parámetros se interpretan del siguiente modo. Diego López recibía 9.34 tiros hasta que le metían un gol el resto de porteros que tuvo el Espanyol en ese año y los siguientes requerían 9.34*0.75 = 7 y claro, con alguno de esos porteros y con la ayuda de actuaciones arbitrales al final el Espanyol terminó en segunda división.