Modelos GAM con R. Dejando satisfechos a los equipos de negocio

Los modelos GAM (Generalized Additive Model) son el conjuntos de modelos que tenemos los estadísticos, actuarios, data scientist o como nos denominen en el momento que leas esto para dejar a nuestros equipos de negocio contentos con los resultados de nuestro modelo GLM. No voy a entrar en los aspectos teóricos de este tipo de modelos, hay documentación como esta que os puede ayudar. Por qué se quedan contentos los equipos de negocio, porque nos ayudan a dar sentido a los modelos. Retomemos un ejemplo que vimos en otra entrada del blog: https://analisisydecision.es/los-parametros-del-modelo-glm-como-relatividades-como-recargos-o-descuentos/ en esta entrada presentamos como el resultado de un modelo GLM se transforma en una relatividad, en un mecanismo para ofrecer recargos y descuentos.

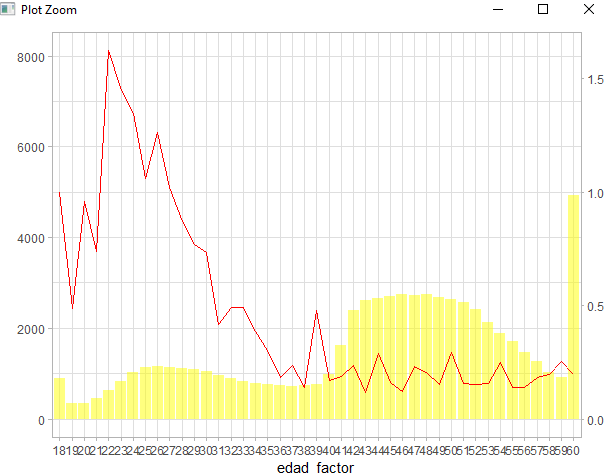
Si desarrollamos un modelo GLM en último término podríamos enseñar este gráfico al responsable comercial:

Parece evidente que a mayor edad mayor proporción de siniestros, además, a partir de los 40 – 45 puede considerarse que las relatividades no varían. Se aprecian tendencias, pero no tiene sentido de negocio aplicar directamente los resultados de las estimaciones, no podemos aplicar esas relatividades obtenidas, es necesario realizar un suavizado y seguramente nos veríamos tentados, una vez hecho el modelo, de aplicar unos suavizados posteriores a la obtención de los parámetros. Podríamos hacer:

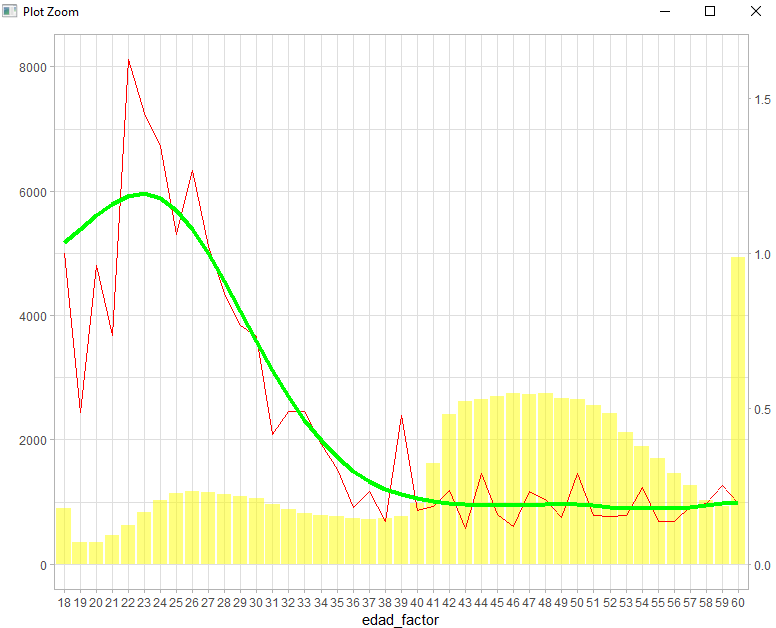
#g2 es el gráfico anterior obtenido en https://analisisydecision.es/los-parametros-del-modelo-glm-como-relatividades-como-recargos-o-descuentos/

spline_edad_factor <- smooth.spline(relatividades$rela,w=relatividades$exp,spar=0.65)
g2 + geom_line(aes(y=spline_edad_factor$y *5000), group=1, color="green",size=1.5)

Con smoot.spline hacemos una función de suavizado para nuestras relatividades, el nivel del suavizado lo controlamos con el parámetro spar que va desde 0 (sin suavizado) a 1 (función lineal). El caso es que el resultado de ese suavizado ya podría tener un mayor sentido de negocio y tendríamos más contentos a nuestro equipo comercial, pero... lo estamos haciendo a posteriori, eso no es una estimación, es echar balones fuera. Bien, qué os parece si tenemos un mecanismo para hacer una función previa a la estimación, pues este mecanismo se denomina modelo GAM y la librería de R que vamos a emplear para aproximarnos a ellos es mgcv. Vamos a replicar el modelo más básico con la edad del conductor.

Modelo GAM con R y la librería mgcv

library(mgcv)

moto$edad_numero <- as.numeric(moto$edad)

gam.1 <- gam(nsin ~ s(edad_numero,bs="cr",k=3) , data=filter(moto,exposicion>0), 
             offset = log(exposicion), family = poisson(link='log'))
summary(gam.1)
plot(gam.1, se=TRUE, col="blue", pages=1)

Dejamos claro que estimamos un número y este número tendrá un orden, aspecto muy importante, la definición del modelo es similar a la que hacemos con glm pero en el momento que ponemos s() queremos que el modelo realice una función de smooth (suavizado) de la edad. Con el parámetro bs especificamos que tipo de función vamos a aproximar, tenemos multitud de posibilidades, incluso las podemos hacer nosotros, en este caso seleccionamos "cr" cubic regression, lo más habitual, si empleamos este tipo de modelos para ajustar curvas de supervivencia hay que poner más cariño en este parámetro. Una vez hemos decidido que hacemos una cubic necesitamos el grado del polinomio de la curva, esto lo hacemos con el parámetro k. Si vemos la sumarización del modelo obtenido:

> summary(gam.1)

Family: poisson 
Link function: log 

Formula:
nsin ~ s(edad_numero, bs = "cr", k = 3)

Parametric coefficients:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept) -4.66642    0.04341  -107.5   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Approximate significance of smooth terms:
                 edf Ref.df Chi.sq p-value    
s(edad_numero) 1.935  1.996  434.9  <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

R-sq.(adj) =  -0.00134   Deviance explained = 5.81%
UBRE = -0.89967  Scale est. = 1         n = 62474

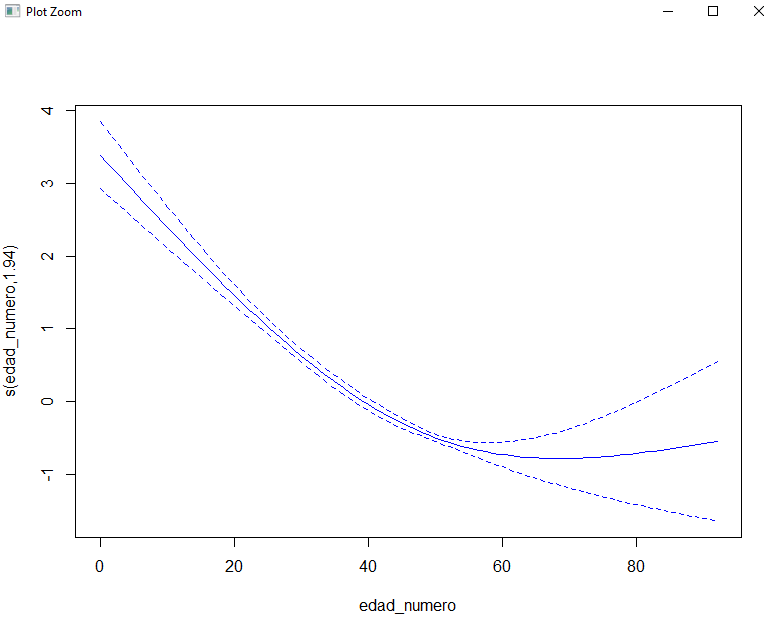
No tenemos factores, incluso en los coeficientes no sale la edad suavizada, aparece como smooth term, aunque tiene su correspondiente p-valor asociado. Con plot obtenemos una visualización de las variables que hemos suavizado y en este caso es muy relevante la opción se=TRUE para ver los intervalos de confianza:

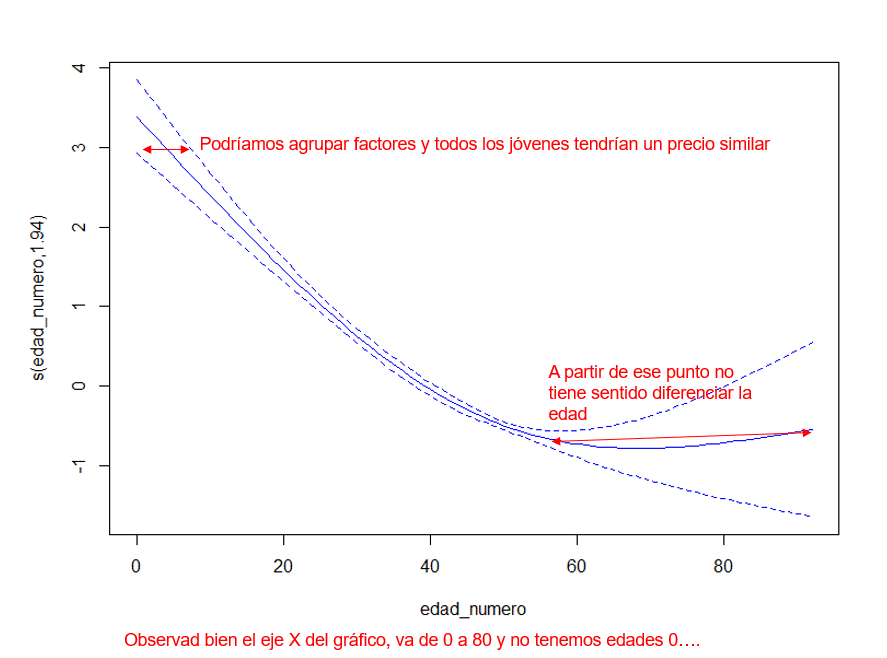
Este gráfico es de vital importancia, vamos a pintar sobre él para que entendáis mejor porque es tan importante un intervalo de confianza:

Si varios puntos de nuestra variable regresora están dentro del intervalo de confianza es recomendable agrupar esos puntos, los intervalos de confianza no están para hacer bonitos los gráficos, nos mejoran las estimaciones y mejoran la consistencia de nuestros modelos (esto no lo hace un XG-Boost). Y muy importante, observad el eje X los valores que tiene, no se corresponden con los valores de la edad, se corresponden con el orden de la variable edad, esto es vital para entender un modelo GAM porque lo que hacen es un suavizado en función del orden, ojo con las interpretaciones que dais a este gráfico porque no es a partir de los 55 años el momento en el que hay que agrupar la edad.

El análisis de legibilidad de la entrada me está advirtiendo que es demasiado larga, me dejo en el tintero muchas cosas como las iteraciones con las variables en estos modelos, qué pasa con las interacciones y como obtenemos relatividades a partir de estos modelos. Espero ir resolviendo esas dudas en próximas entradas.