Modelos lineales dinámicos (DLM) con R

Otro de los modelos que está tocando estudiar este verano son los Dinamic Linear Models (DLM). Para estudiar este tipo de modelos es imprescindible leer este documento.  Estos métodos parten de una idea: «la vida no es fácil cuando tienes que hacer estimaciones sobre una serie temporal». Una serie temporal es un vector de datos aleatorios, una sucesión de observaciones de la forma Yt con t=1,2,.. Si sobre esta  sucesión tenemos una característica que puede influir estamos ante un modelo de espacio estado. Estos modelos tienen  una cadena de Markov (http://es.wikipedia.org/wiki/Cadena_de_M%C3%A1rkov) porque esa característica que afecta a la serie es una cadena de Markov y eso nos permite que los Yt sean independientes ya que dependen sólo de esa característica. El más importante modelo de espacio estado es el modelo lineal dinámico.

Los modelos lineales dinámicos vienen representados por una ecuación de observación Yt=F’·Bt + Vt con Vt según N(0,vt) y una ecuación de sistema o ecuación de estado Bt = Gt·Bt-1 + wt  con wt según N(0,wt). Luego está caracterizado por F y G que son matrices conocidas, B es un vector de parámetros desconocidos , Vt es la varianza de la ecuación de observaciones y Wt la varianza de la ecuación del sistema, ambas conocidas. El modelo más sencillo de este tipo es el paseo aleatorio, un modelo que no presenta estacionalidad ninguna. Sin entrar mucho más en temas matemáticos si es importante comentar que esta técnica la emplearemos tanto para filtrar, suavizar y predecir.

Ahora vamos a dar comienzo con el trabajo en R a ver si podemos analizar el número de visitas que recibe esta web desde abril de 2008 hasta julio de 2014.

# Objeto con las visitas
visitas=c(213,376, 398, 481,416, 505, 771, 883,686, 712 ,
883,993,1234 , 1528 ,1965 ,1676 ,1037 , 1487 ,1871 ,2725 ,2455 ,2856 ,
2868,2809 ,3326 ,4284 ,4599 ,3863 ,3778 ,5090 ,5510 ,5911 ,4460 ,5495 ,5290 ,
6407,5619 ,6494 ,5854 ,4940 , 4735 ,6049 ,6839 ,8695 ,7112 ,9207 ,8991 , 10909 , 9647 , 10943 , 9819 , 8982 ,
8597,10004,12550,12025, 9108,10664, 9563,9751 ,11402 ,11875,10395,
10078,8706,10893, 13197,12868 ,9857 ,12119 , 13421 ,14411, 12820 , 14443 , 12713 ,
13869)

#Creacion de la serie temporal desde abril de 2008 a julio de 2014
serie <- ts(visitas, start=c(2008, 4), end=c(2014, 7), frequency=12)
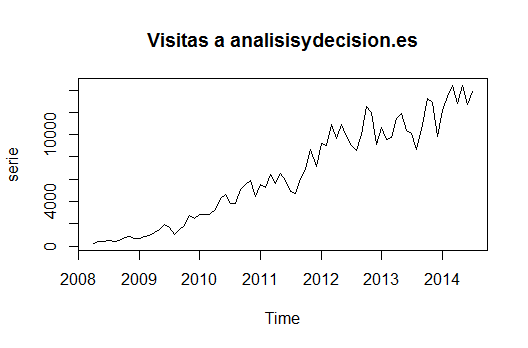
plot(serie,main=»Visitas a analisisydecision.es»)

#install.packages(«dlm»)
library(dlm)

modelo.polinomico = dlmModPoly(order=1,dV=1000,dW=100)
serie.filtrada = dlmFilter(serie,modelo.polinomico)

str(modelo.polinomico)
str(serie.filtrada,1)

Con la función dlmModPoly creamos un objeto que contiene las características del modelo que deseamos generar, un modelo de paseo aleatorio con varianza V para las observaciones de 1000 y con varianza para los estados de W. Estas características son:
List of 10
m0 : num 0 C0 : num [1, 1] 1e+07
$ FF : num [1, 1] 1
$ V : num [1, 1] 1000
$ GG : num [1, 1] 1
$ W : num [1, 1] 100
JFF: NULL JV : NULL
JGG: NULL JW : NULL
– attr(*, «class»)= chr «dlm»

Nosotros hemos especificado el orden del polinomio. La varianza de las observaciones dV y la varianza de los estados dW. Los datos que hemos asignado a estas varianzas han sido seleccionados de forma azarosa para no alargar la entrada del blog. Con estas especificaciones podemos realizar un filtrado mediante el filtro de Kalman  sobre la serie y representar gráficamente los resultados obtenidos:

serie.filtrada = dlmFilter(serie,modelo.polinomico)
str(serie.filtrada,1)
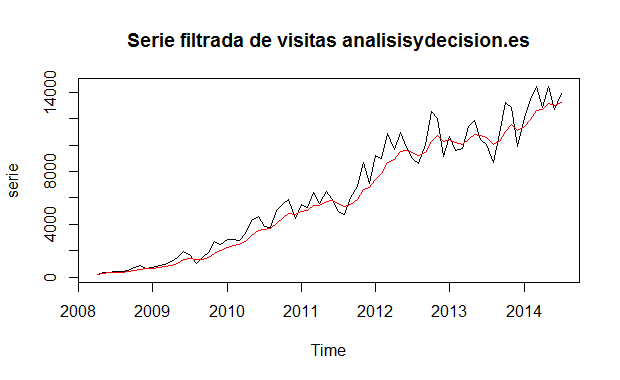
plot(serie,main=»Serie filtrada de visitas analisisydecision.es»)
lines(dropFirst(serie.filtrada$m), col=’red’)

Observamos como realiza el filtro de Kalman de  la serie el modelo con la función dlmFilter. Esta función genera un objeto lista dlm con las siguientes características:
List of 9
$ y : Time-Series [1:76] from 2008 to 2014: 213 376 398 481 416 505 771 883 686 712 …
Se trata de la serie de datos con todas sus 76 observaciones
mod:List of 10
..- attr(*, «class»)= chr «dlm» m : Time-Series [1:77] from 2008 to 2014: 0 213 298 337 384 …
m contiene la media de la distribución de los valores filtrados del vector de estados, tiene 77 elementos porque empieza en el 0 siempre antes de la primera observacion
U.C:List of 77 D.C: num [1:77, 1] 3162.3 31.6 22.9 19.6 18.1 …
U.C y D.C  contienen la descomposición en valores singulares de la varianza de los errores de filtrado UC es una lista de matrices y DC es una matriz
$ a : Time-Series [1:76] from 2008 to 2014: 0 213 298 337 384 …
a es el vector que incluye las medias de las estimaciones del modelo
U.R:List of 76 D.R: num [1:76, 1] 3162.3 33.2 25 22 20.6 …
U.R y D.R contienen descomposición de la matriz de errores de predicción y pueden ser útiles para reconstruir varianzas
$ f : Time-Series [1:76] from 2008 to 2014: 0 213 298 337 384 …
f contiene la serie con la predicción un paso adelante de nuestro modelo. Tiene 76 observaciones porque no hay estimación para el primer elemento
– attr(*, «class»)= chr «dlmFiltered»

Cuando realicemos filtrados sobre series es muy importante la relación entre dW/dV, cuanto menor sea esta relación los datos de filtrado estarán más próximos a la serie. Veamos un ejemplo:

plot(serie,main=»Análisis de la relación W/V con la serie
de visitas a analisisydecision.es»)
modelo.polinomico = dlmModPoly(order=1,dV=1000,dW=100)
serie.filtrada = dlmFilter(serie,modelo.polinomico)
lines(dropFirst(serie.filtradam), col=’red’)
modelo.polinomico = dlmModPoly(order=1,dV=100,dW=100)
serie.filtrada = dlmFilter(serie,modelo.polinomico)
lines(dropFirst(serie.filtradam), col=’blue’)

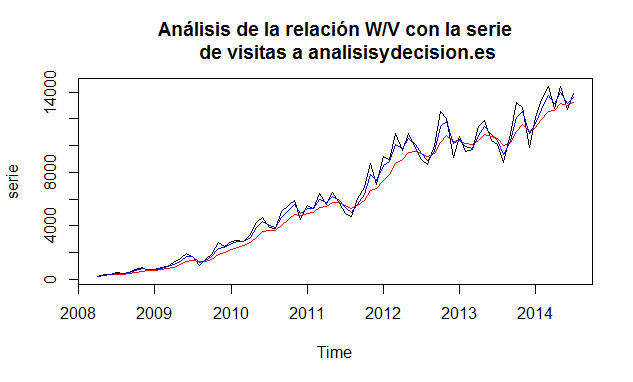Vemos que la línea roja pinta nuestro filtrado más alejado de las observaciones porque la relación entre la varianza de los estados entre la varianza de las observaciones es 10. Sin embargo si reducimos a 1 esta relación tenemos un filtrado muy próximo a la serie, representado en la línea azul.

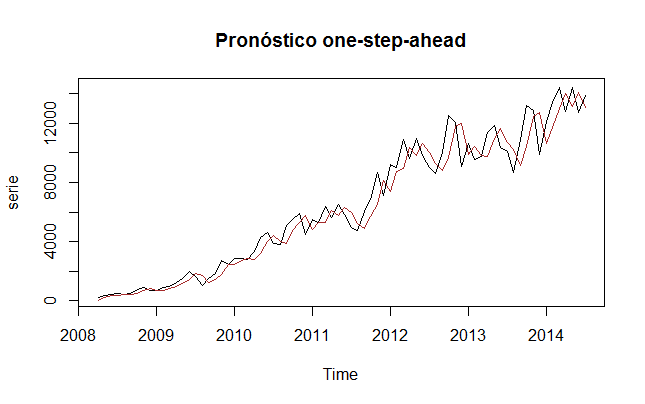
Para la realización de estimaciones tenemos el elemento f [forecast] del objeto dlm serie.filtrada podemos ver gráficamente como funcionan nuestros pronósticos «un-paso-adelante»:
#Pronosticos
modelo.polinomico = dlmModPoly(order=1,dV=1500,dW=3000)
serie.filtrada = dlmFilter(serie,modelo.polinomico)

plot(serie,main=»Pronóstico one-step-ahead»)
lines(serie.filtrada$f,col=»brown»)

Si deseamos realizar un suavizado de nuestra serie tenemos que emplear la función dlmSmooth, esta función calcula los valores suavizados junto con las varianzas de los errores del suavizado. Es interesante ver  la diferencia entre la varianza de los errores de filtrado frente a la varianza de los errores de suavizado:

#Errores de suavizado
attach(serie.suavizada)
suavizado=sqrt(unlist(dlmSvd2var(U.S, D.S)))
detach(serie.suavizada)

#Errores de filtrado
attach(serie.filtrada)
filtrado=sqrt(unlist(dlmSvd2var(U.C, D.C)))
detach(serie.filtrada)

compara=data.frame(cbind(suavizado,filtrado))

Para ver los valores de la descomposición de la varianza empleamos la función dlmSvd2var. Observando la serie vemos que la varianza de los errores para la serie filtrada es mayor que en el caso de la serie suavizada. En t=1 la varianza  para la serie  de filtrado es desmesurada. Esto sucede porque la serie suavizada emplea todos los datos de la serie, sin embargo la serie filtrada para el paso n emplea hasta n+1 por ello en el último paso las varianzas coinciden ya que están empleando el mismo número de observaciones, el total. Hasta aquí un breve resumen de las posibilidades que tenemos con la librería dlm de R. Espero que despierte vuestra curiosidad. En mi caso concreto ha servido de acercamiento al análisis de series temporales, mi gran laguna. Tengo que empezar a trabajar con ellas. Saludos.