Para un tema de mi trabajo voy a utilizar una regresión de poisson en vez de una regresión logística, el evento es si o no y no tiene nada que ver el tiempo, ni se puede contabilizar como un número, pero a efectos prácticos es mejor para mi usar una regresión de poisson. Entonces, ¿qué pasa si hago una poisson en vez de binomial? Como siempre si mi n es muy grande hay relación entre ambas distribuciones. Pero yo quiero saber si me puede clasificar mis registros igual una regresión de poisson y una binomial y se me ha ocurrido hacer un ejercicio teórico muy simple.
Construyo con SAS 10.000 datos aleatorios con las variables independientes x e y normalmente distribuidas y la variable dependiente z que es una función logística «perfecta» de x e y:
data logistica;
do i=1 to 10000;
x=rannor(8);
y=rannor(2);
prob=1/(1+exp(-(-10+5*x-5*y)));
z=ranbin(8,1,prob);
output;
end;
drop i;
run;
data entrenamiento test;
set logistica;
if ranuni(6)>0.8 then output test;
else output entrenamiento;
run;
proc freq data=entrenamiento;
tables z;
quit;
Separo los datos en entrenamiento y test y vemos que un 8% aproximadamente de mis registros tienen valor 1. Sobre estos datos hago una logística y una poisson y veo los parámetros:
proc logistic data=entrenamiento;
model z=x y;
quit;
proc genmod data=entrenamiento ;
model z = x y / dist = poisson link = log scale=deviance;
run;
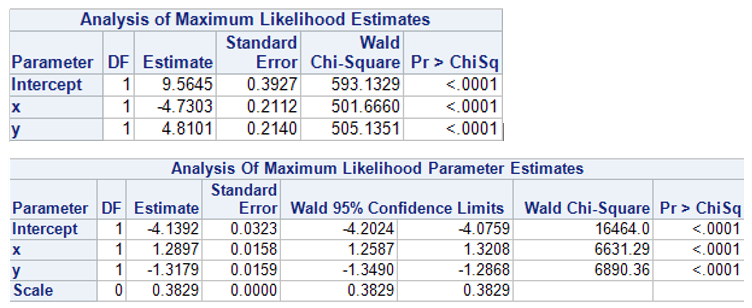
Los parámetros no tienen porque parecerse claro pero si me gustaría que observarais que tienen signo contrario, un apunte. Ahora, tal cual me han salido, hacemos un scoring sobre los datos de test y dividimos en 10 tramos por esas variables de scoring:
data test;
set test;
prob_logistica=1/(1+exp(-(-9.5645+4.7303*x-4.8101*y)));
num_poisson = exp(-4.1392 + 1.2897*x + -1.3179*y);
run;
proc rank data=test out=test2 groups=10;
var prob_logistica;
quit;
proc rank data=test2 out=test2 groups=10;
var num_poisson;
quit;
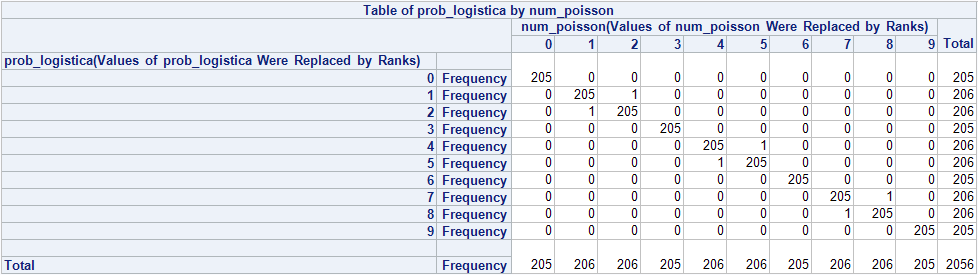
Creo el scoring «a lo mecagüen» como le gusta decir a mi amigo Juan y en otro dataset tengo las variables prob_logistica y num_poisson resultantes del scoring divididas en 10 tramos, si hacemos una tabla de frecuencias de estas dos variables obtenemos:
proc freq;
tables prob_logistica*num_poisson/nocol norow nopercent;
quit;
Resulta que obtenemos prácticamente lo mismo, así que puedo usar la poisson en vez de la binomial y hablar de proporciones en vez de probabilidades, algo que explica mejor mi problema.
Estimado, muy interesante tu blog!
La verdad no encontré la forma de escribirte un mensaje de forma privada, así que lo hago por aquí.
Necesito ayuda para realizar alguna sentencia con SAS (no se programar macros) que haga lo siguiente:
Construir un pedigree a partir de un data set como el siguiente (por ej.)
individuo padre madre
3 1 2
10 3 4
11 7 8
13 11 10
16 11 6
Y el pedigree reconstruido tendría que quedar de la siguiente manera:
individuo padre madre
1 0 0
2 0 0
3 1 2
4 0 0
6 0 0
7 0 0
8 0 0
10 3 4
11 7 8
13 11 10
16 11 6
NOTA: el «0» sería un dato missing.
Se entiende lo que estoy buscando?
Bueno, espero que me puedas ayudar y no sea mucha molestia.
Desde ya gracias.
Saludos
Alan
Siguiendo con el ayuda anterior, la otra cuestión que me intriga es si se puede de alguna forma ingresar un individuo «interés» a alguna sentencia y que a partir de allí reconstruya el pedigree total relacionado a ese individuo.
Por ej. (partiendo del pedigree anterior):
Quisiera saber el pedigree total del individuo 13.
Tiene que quedar de la siguiente manera:
individuo padre madre
3 1 2
4 0 0
7 0 0
8 0 0
10 3 4
11 7 8
13 11 10
Espero no abusar con esto!
gracias!
Le echo un vistazo Alan.
Hola Raul,
Igual es una duda un poco de base, porque nunca he utilizado dis de Poisson, pero según tengo entendido la regresión logística binomial es para eventos de tipo (0/1) y la de Poisson para cuando hay varios posibles valores. Ejemplo, en seguros, binomial para ver la probabilidad de un siniestro y la de Poisson para calcular número de siniestros en un periodo (1,2,3…)
¿Es correcto aplicar Poisson en tu caso?, aprovecho para preguntarte más cosas:
Al poner link=log , se aplica transformación logarítmica a la variable resultado
ln(x) = a0 + a1x +a2y + a3z…
¿es correcto?
No entiendo en bien el papel que juega la distrbución de Poisson en este modelo,
¿lo puedes explicar?
Gracias,
No tiene sentido usar una poisson, pero si haces el ejercicio teórico resulta que te sale lo mismo. Cuando n es muy grande la binomial(n,p) se aproxima a la poisson cuyo lambda es n*p y puede interesarnos usar esta distribución.
En mi caso, el motivo por el que hice este ejercicio, era mejor obtener proporciones o frecuencias en vez de probabilidades y por ello empleo la poisson. La transformación exponencial y logarítmica la pongo para que se entienda como se pasan parámetros de los modelos y para que se vea como varían. Y el error estándar de los parámetros también es interesante porque la estimación de la poisson es más conservadora.
Saludos.