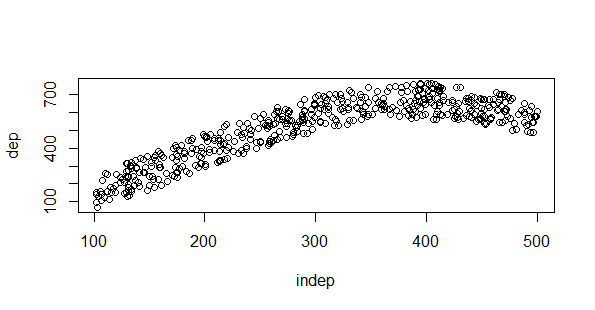
Hace mucho planteé un juego de identificación de modelos con R y ya se me había olvidado daros la solución. Pensando en el Grupo de Usuarios de R y en hacer algo parecido en una presentación recordé que había que solucionar el ejercicio. Lo primero es la creación de los datos, se me ocurrió una función sencilla y una nube de puntos alrededor de ella:
#Variable independiente
indep = runif(500,100,500)
#Función para crear la variable dependiente
foo = function(x){ mean(x)*(1-sin(-0.006042*x))
}
dep = sapply(indep,foo)
dep=dep+(runif(length(dep),-100,100))
datos = data.frame(cbind(indep,dep))
plot(datos)
Seleccionamos los datos de entrenamiento y test:
#Datos de entrenamiento y test indices = sample(1:length(dep),length(dep)/2) entrenamiento = datos[indices,] test = datos[-indices,]
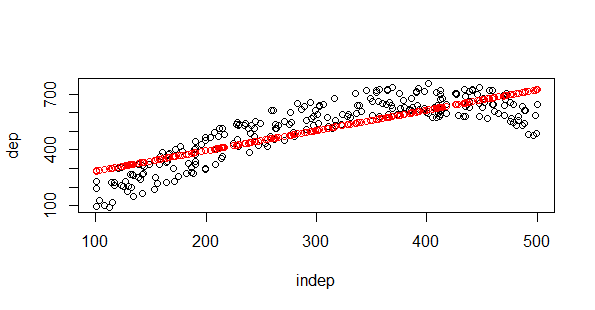
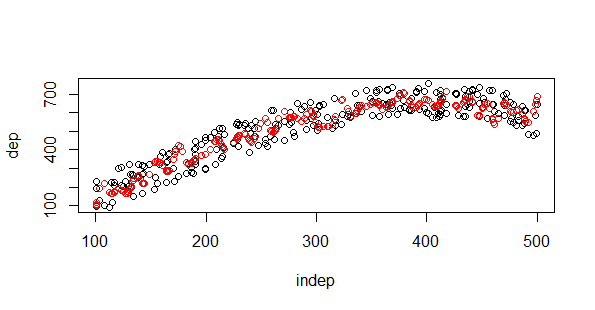
El más sencillo de todos era el caso de la regresión lineal y fue el que puse de ejemplo:
#REgresión lineal modelo.1=lm(dep ~ indep,entrenamiento) plot(test) points(test$indep,predict(modelo.1,test),col="red")
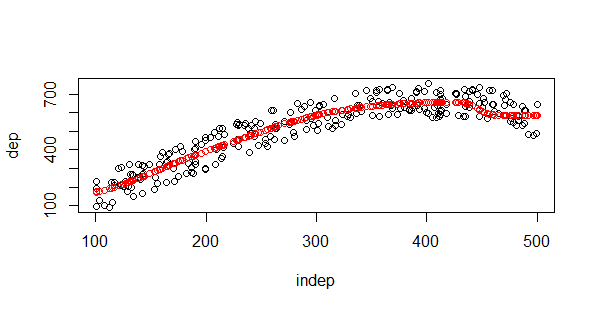
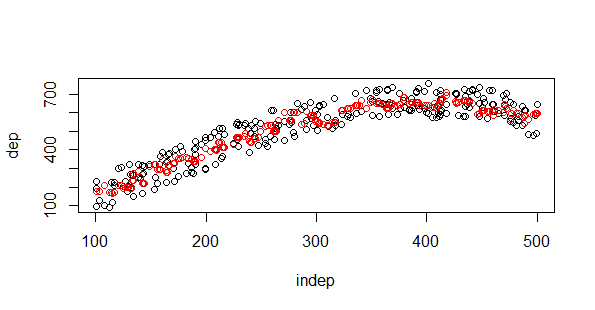
Una línea que pasa por la media de la nube de puntos. Otro de los casos menos complicados es el árbol de regresión:
#Arbol de decision library(rpart) modelo.2=rpart(dep~indep,entrenamiento, control=rpart.control(minsplit=20, cp=0.002, xval=100) ) plot(test) points(test$indep,predict(modelo.2,test),col="red")
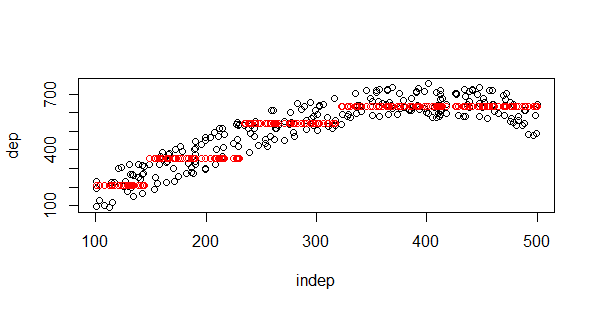
En los árboles de decisión podemos jugar con el parámetro de complejidad cp:
#Arbol de decision library(rpart) modelo.2=rpart(dep~indep,entrenamiento, control=rpart.control(minsplit=20, cp=0.02, xval=100) ) plot(test) points(test$indep,predict(modelo.2,test),col="red")
Observad que a los árboles les “cuesta una peonada” salir de la nube de puntos en sus estimaciones. Mis queridas redes neuronales siempre necesitan más trabajo, pero es muy interesante como salva la linealidad nnet con una sóla neurona y 5 nodos:
#Redes neuronales
library(nnet)
#Función para encontrar la mejor red neuronal en base a la menos sscc
mejor.red {
mejor.rss for(i in 1:50){
modelo.rn linout=T, trace=F,decay=0.2)
if(modelo.rnvalueindep,predict(modelo.3,test),col="red")
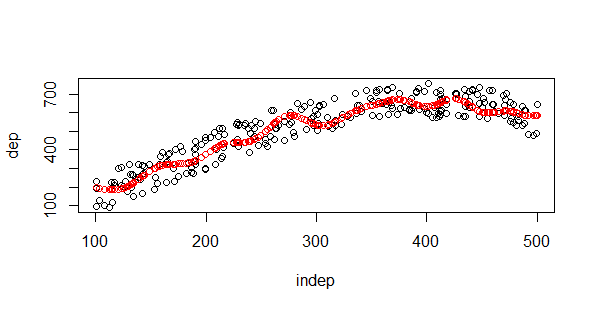
Necesitamos seleccionar el mejor modelo y lanzamos 50 iteraciones, obtenemos un gran ajuste, recordamos que linout=T porque estamos con una regresión y no con una clasificación. Empezamos con los “sobreajustadores” el primero el SVM:
#SVM library(e1071) modelo.4=svm(dep ~ indep ,entrenamiento, method="C-classification", kernel="radial",cost=100,gamma=100) plot(test) points(test$indep,predict(modelo.4,test),col="red")
Venga me he pasado con los parámetros de ajuste para dejar mal a los SVM, si soy un poco menos listo podemos hacer:
modelo.5=svm(dep ~ indep ,entrenamiento, method="C-classification",
kernel="radial",cost=10,gamma=10)
plot(test)
points(test$indep,predict(modelo.5,test),col="red")
Con sobreajuste los SVM puede ofrecer alguna estimación fuera de la nube de puntos, sin embargo siendo menos estrictos con esos parámetros los SVM quedan siempre dentro de la nube de puntos y su estimación se parece mucho a la que pueda ofrecernos una red neuronal. El KNN tampoco va a sacar ningún punto del test de la nube de puntos:
#knn
library(kknn)
modelo.6 k = 4, kernel = c("rectangular"))
plot(test)
points(test$indep,predict(modelo.6,test),col="red")
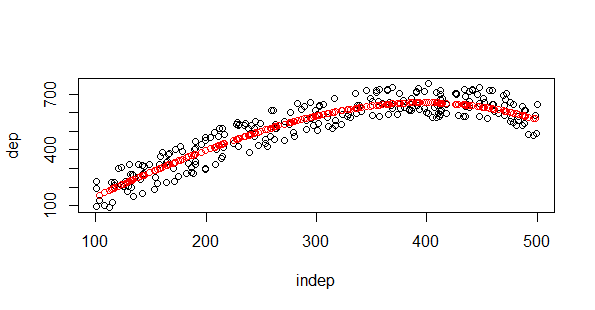
Otro de mis sobreajustadores preferidos y por último el clásico loess que siempre nos ha puesto mucho a los dinosaurios:
#loess modelo.7 plot(test) points(test$indep,predict(modelo.7,test),col="red")
Bueno aquí tenéis el ejercicio con su correspondiente código en R. A ver si dejo un poco de lado estas técnicas y empiezo a trabajar con las técnicas de concursos que tan poco me gustan. Saludos.