Quería plantearos un ejemplo de análisis cluster para observar el peligro que tiene agrupar observaciones en base a grupos homogéneos creados con distancias multivariantes. Para ilustrar el ejemplo trabajamos con R, creamos grupos en base a 2 variables, esto nos facilita los análisis gráficos. Simulamos el conjunto de datos con el que trabajamos:
#GRUPO 1
x = runif(500,70,90)
y = runif(500,70,90)
grupo1 = data.frame(cbind(x,y))
grupo1$grupo = 1
#GRUPO 2
x = runif(1000,10,40)
y = runif(1000,10,40)
grupo2 = data.frame(cbind(x,y))
grupo2$grupo = 2
#GRUPO 3
x = runif(3000,0,100)
y = runif(3000,0,100)
grupo3.1 = data.frame(cbind(x,y))
grupo3.1separacion=(x+y)
grupo3.1 = subset(grupo3.1,separacion>=80&separacion <=140,select=-separacion)
grupo3.1 = subset(grupo3.1,y>0)
grupo3.1grupo = 3
#UNIMOS TODOS LOS GRUPOS
total=rbind(grupo1,grupo2,grupo3.1)
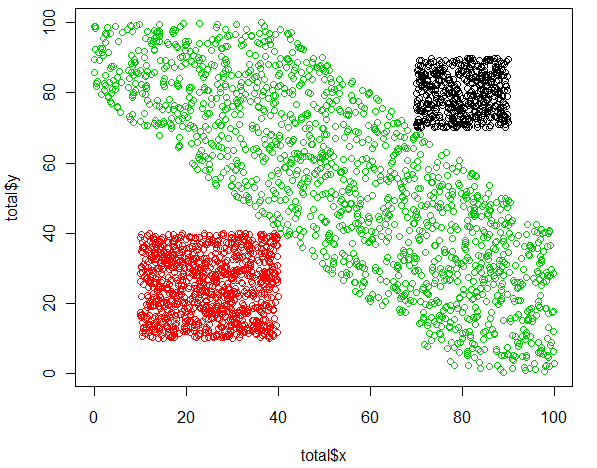
plot(totalx,totaly,col=c(1,2,3)[total$grupo])
Los grupos parecen claros:
Cabe preguntarse: ¿qué sucede si segmentamos en base a centroides? Para responder a esta pregunta hacemos un análisis no jerárquico, empleamos el algoritmos de las k-medias del que ya se ha hablado en este blog en alguna ocasión:
distancias = dist(total)
clus = kmeans(distancias,3)
totalgrupo_nuevo = cluscluster
plot(totalx,totaly,col=c(1,2,3)[total$grupo_nuevo])
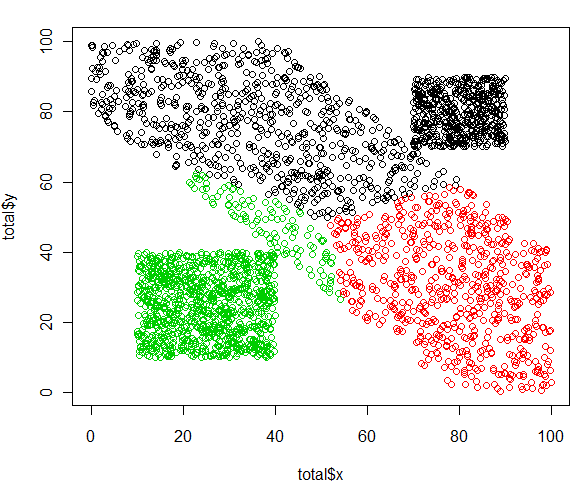
Necesitamos un objeto con las distancias y sobre él utilizamos la función kmeans que es la más popular y sencilla. El objeto resultante de la realización del modelo tiene una variable cluster que añadimos a nuestros datos y tras graficar vemos que es evidente que no ha funcionado muy correctamente, nos ha creado los 3 grupos homogéneos en base a la distancia entre observaciones, pero no son los segmentos deseados… Mucho cuidado cuando utilicemos este tipo de técnicas.
¿Cómo podemos realizar una segmentación más apropiada para estos datos? ¿Qué técnica podemos utilizar? La respuesta en breve. Espero que esto sirva para desordenar alguna conciencia.
Me a parecido interesante este ejemplo. Realmente he mirado varios tipos de clasificación, con estos datos simulados. Pero todos no lo hacen bien. Creería a que se debe a que la gran mayoría de las técnicas de clasificación, se basan en la métrica que se utilice. Sin embargo, métricas como la mahalanobis la cual se basa en calcular la matriz de covarianzas, tampoco lo hace bien -esto debe ser por la homogeneidad de los grupos-.
Estoy intrigado con la técnica de segmentación apropiada. Pensaría en alguna técnica de remuestreo o alguna técnica que detecte grupos outliers.
Interesante.
Hola Alex, circula un video por el mundo que ilustra mejor este problema, pero no le encuentro…
Una pista: imagina que hacemos un algoritmo que «lanza planos» entre las observaciones, parece claro que, en este ejemplo, dos planos identificarían los 3 grupos.
Pingback: Análisis y decisión
Raul sabes algún sitio donde me pueda descargar el sas miner como versión de prueba.
Muchas gracias
La verdad es que lo desconozco, es un software propietario y tiene que ir con su licencia correspondiente. En SAS no tienen costumbre de tener versiones de prueba y en este caso no hay ni versiones de estudiante.
gracias raul
Creo que hay un pequeño inconveniente con lo que muestras, ¿quién necesita un análisis de conglomerados con grupos tan perfectamente definidos? Creo que este tipo de herramientas están diseñadas para problemas en los que no es sencillo determinar un agrupamiento natural en los datos. Y es precisamente eso, no son una bola de cristal que te permite distinguir perfectamente qué individuos están agrupados entre sí.