La representación de variables categóricas en cajas es uno de los gráficos que más utilizo, empezaron a gustarme debido al uso de Qlik Sense y sus gráficos de cajas, me permitían comparar variables categóricas en un periodo frente a otro. En R podemos usar la librería treemap para realizar estos gráficos y comparar variables categóricas. En este caso interesa comparar una variable dentro de dos grupos.
Para ilustrar el ejemplo nos suministran un conjunto de datos con información de un seguro de responsabilidad civil de motocicletas de una compañía sueca. Este conjunto de datos está en la librería CASdatasets de R:
library(tidyverse) library(CASdatasets) data(swmotorcycle)
Nos piden evaluar la variable RiskClass, esta variable es categórica y viene definida como la relación de la potencia de la moto en KW x 100 entre el peso de la moto + 75 kg (peso medio del piloto). Esta relación se divide en 7 clases que son necesarias de evaluar.
Vamos a crear una variable binomial Tiene_siniestro si el importe del siniestro es mayor que 0 tomará «Tiene siniestro», si el importe es <=0 tomará «No tiene siniestro». Y mediante la librería de R treemap compararemos la exposición al riesgo de cada grupo Tiene_siniestro x RiskClass. Para llevar a cabo esta comparativa usaremos un gráfico de cajas
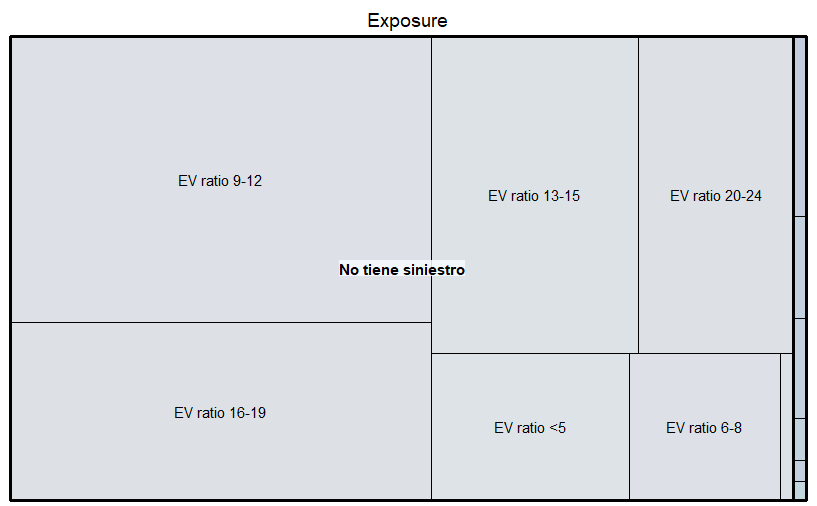
. Inicialmente hacemos el gráfico para esas dos variables:
swmotorcycle <- swmotorcycle %>%
mutate(Tiene_siniestro = ifelse(ClaimAmount>0, "Tiene siniestro", "No tiene siniestro"))
library(treemap)
library(RColorBrewer)
p <- treemap(swmotorcycle,
index=c("Tiene_siniestro","RiskClass"),
vSize="Exposure",
type="index",
fun.aggregate = "sum",
palette = "Blues")
Este gráfico no tiene ni pies ni cabeza, no se puede ver absolutamente nada, de nuevo la importancia de relativizar los grupos, es necesario calcular porcentajes dentro de aquellos que tienen siniestros y porcentajes de los que no tienen siniestros, afortunadamente para la compañía de seguros pocos expuestos tienen siniestros. Veamos un ejemplo para calcular porcentajes entre grupos con dplyr:
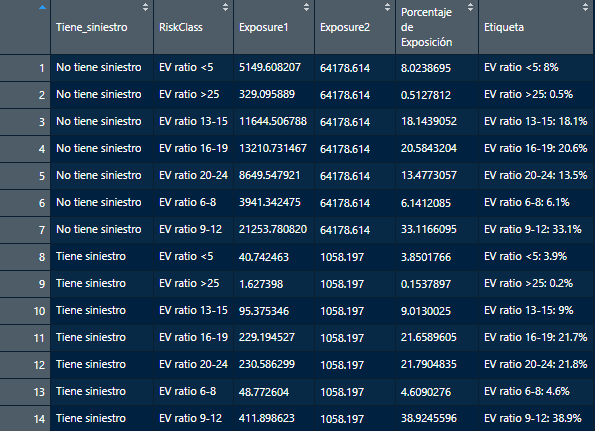
swmotorcycle %>% group_by(Tiene_siniestro,RiskClass) %>% summarise(Exposure1=sum(Exposure))%>%
left_join(swmotorcycle %>% group_by(Tiene_siniestro) %>% summarise(Exposure2=sum(Exposure))) %>%
as_tibble() %>%
mutate('Porcentaje de Exposición' = (Exposure1/Exposure2)*100,
Etiqueta = paste0(RiskClass, ': ', round(`Porcentaje de Exposición`,1), '%')) -> resumen
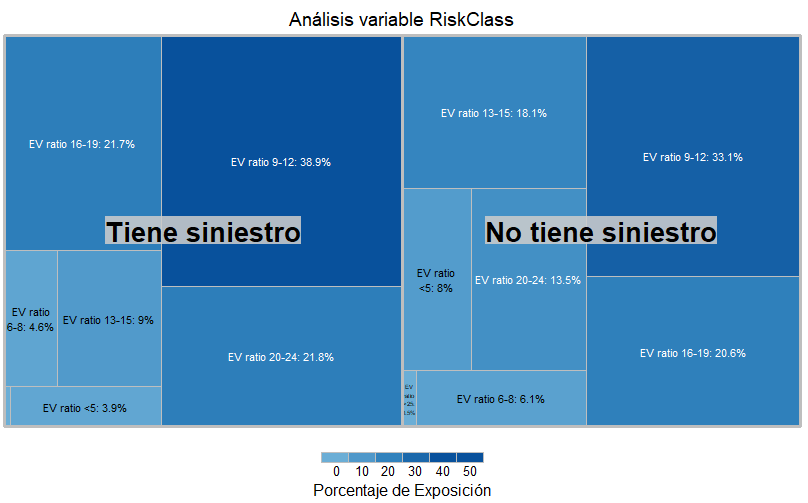
Lo que hacemos es calcular el agregado de exposición de los grupos, unimos con el agregado de los subgrupos y eso nos permite calcular el porcentaje de exposición dentro de cada grupo. Aprovechamos y generamos una variable para la etiqueta del gráfico. En este punto nuestro gráfico puede ser más representativo:
p <- treemap(resumen,
index=c("Tiene_siniestro","Etiqueta"),
vSize='Porcentaje de Exposición',
vColor='Porcentaje de Exposición',
type="value",
range = c(0,50),
fontsize.labels=c(20, 8),
title = "Análisis variable RiskClass",
mirror.x = T,
palette = brewer.pal(n=5,"Blues"),
border.col = "grey")
Este es el gráfico que abre la entrada, los parámetros más relevantes de la función treemap son:
- index: Especificamos las variables a presentar, es importante el orden. Hemos creado un campo etiqueta para ver el dato.
- vSize y vColor: indican la medida a representar.
- type: es importante porque el tamaño lo define el valor no una agregación como en el primero de los treemap.
En este caso vemos que los grupos de ratio 9-12 y ratio 20-24 son los que más presencia tienen entre los que han tenido siniestros. Cabía esperar este resultado, el grupo entre 9-12 son motos poco potentes pero con mayor uso y las motos con el indicador entre 20 y 24 son las más potentes y es probable que tengan mayor siniestro, sobre todo si se trata de datos de nuevo negocio como parece ser el caso.