La pasada semana, en un examen, me preguntaron cuál era el mejor punto para una prueba diagnóstica; era necesario razonar mi respuesta. Seguramente mi respuesta fue correcta pero mi razonamiento no lo fue y por eso quería redimirme. Para evaluar las pruebas diagnósticas con una respuesta binaria si/no contamos con la sensibilidad y la especificidad. La sensibilidad es la capacidad que tiene la prueba para acertar sobre los que de verdad tiene que acertar, la probabilidad de etiquetar como enfermos aquellos que verdaderamente están enfermos. La especificidad es una medida que nos indica cuanto nos hemos equivocado con los “unos”, la probabilidad de etiquetar enfermos a pacientes sanos. Una forma de medir cuanto acertamos y cuanto nos equivocamos con nuestra prueba. Para analizar el comportamiento de nuestra prueba diagnóstica debemos determinar un punto de corte. Para ilustrar como seleccionar el mejor punto de corte vamos a emplear unos datos sacados de la web de bioestadística del Hospital ramón y Cajal y vamos a elaborar una curva ROC con R y ggplot2.
La curva ROC es una representación gráfica de la sensibilidad y uno menos la especificidad. ROC es el acrónimo de Reciver Operating Characteristic. Es un método para valorar como está funcionando nuestro método diagnóstico, cuanto mejor es si lo comparamos con el azar. El azar diría que tenemos las mismas probabilidades de tener cualquier tipo de diagnóstico, es decir pintamos una línea recta del punto (0,0) al punto (1,1) eso es el puro azar. En la red tenéis mucha literatura al respecto de divulgadores mejores que yo.
Ejemplo que habíamos comentado: Evaluación del volúmen corpuscular medio (VCM) en el diagnóstico de anemia ferropénica. Se usa como «patrón de oro» la existencia de depósitos de hierro en la médula ósea
Introducimos los datos mediante la lectura más sencilla, no son muchos:
sin = scan()
52 58 62 65 67 68 69 71 72 72 73 73
74 75 76 77 77 78 79 80 80 81 81 81 82 83
84 85 85 86 88 88 90 92
sin = data.frame(sin,rep(0,length(sin)))
names(sin)=c("medida","Fe")
con = scan()
60 66 68 69 71 71 73 74 74 74 76 77
77 77 77 78 78 79 79 80 80 81 81 81 82 82
83 83 83 83 83 83 83 84 84 84 84 85 85 86
86 86 87 88 88 88 89 89 89 90 90 91 91 92
93 93 93 94 94 94 94 96 97 98 100 103
con = data.frame(con,rep(1,length(con)))
names(con)=c("medida","Fe")
datos = data.frame(rbind(sin,con))
Para analizar la sensibilidad y la especificidad de nuestra tenemos que establecer unos puntos de corte y elaborar para cada punto de corte una tabla 2×2 de este modo:
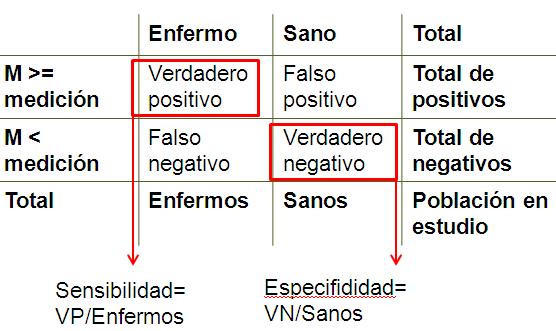
Vamos a realizar una tabla 2×2 para todos los puntos de corte de la medida del VCM que van desde 60 hasta 95, almacenamos en un objeto los valores de la sensiblidad y la especificidad para posteriormente poder realizar la representación gráfica:
rm(resultados)
for (i in seq(60,95,by=5)){
tabla_2.2 = table(ifelse(datosmedida>= i ,1,0),datosFe)
sensibilidad = tabla_2.2[1,1]/(tabla_2.2[1,1]+tabla_2.2[2,1])
especificidad= tabla_2.2[2,2]/(tabla_2.2[1,2]+tabla_2.2[2,2])
if (i == 60) resultados = c(i,sensibilidad,1-especificidad)
else resultados = rbind(resultados,c(i,sensibilidad,1-especificidad)) }
resultados = data.frame(resultados)
Los resultados obtenidos con nuestra prueba quedan tabulados del siguiente modo:
X1 X2 X3 1 60 0.05882353 0.00000000 2 65 0.08823529 0.01515152 3 70 0.20588235 0.06060606 4 75 0.38235294 0.15151515 5 80 0.55882353 0.28787879 6 85 0.79411765 0.56060606 7 90 0.94117647 0.74242424 8 95 1.00000000 0.92424242 library(ggplot2) p <- ggplot(resultados, aes(x = X3, y=X2)) + geom_line() p + geom_abline(intercept=0, slope=1, colour="red")library(ggplot2)
La primera variable son los puntos de corte seleccionados, la segunda la sensibilidad y la tercera 1 – la especificidad. Así pues si graficamos sensibilidad frente a 1-especificidad tenemos la curva ROC:
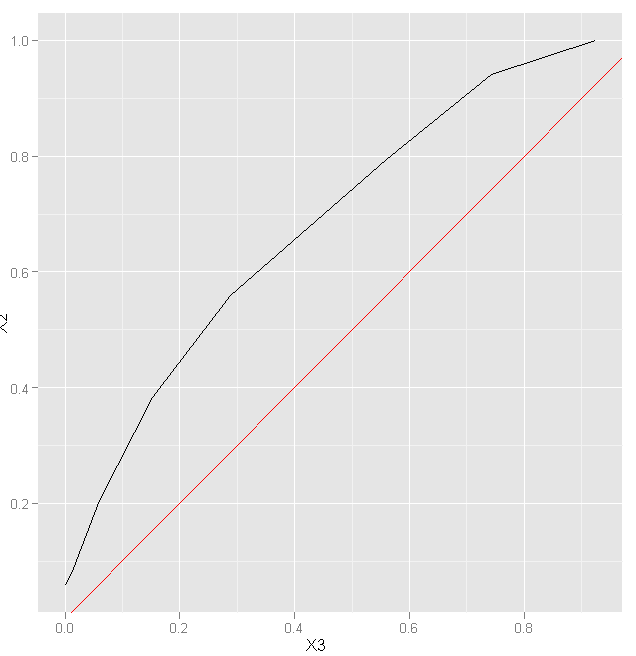
Pintamos la curva ROC para los puntos de corte establecidos. Y ahora viene el punto en el que me redimo de la contestación del examen que hice que seguro que suspenderé porque mis problemas de memoria son bastante graves. El punto de corte óptimo es aquel donde es máxima la diferencia sensibilidad -(1-especificidad). Es decir, donde menos errores cometemos a la hora de hacer el diagnóstico y donde menos etiquetamos de forma incorrecta a los que no tienen la enfermedad, donde mejor separamos. Aquí ya me equivoqué en el examen, pero además es muy importante determinar para que estamos empleando nuestro análisis. Todo lo que está escrito arriba no sirve de nada si no sabemos el objeto del análisis.
¿Para qué estamos haciendo la prueba? Si estamos identificando aquellos pacientes que tienen un cáncer me importa menos la especificidad, si etiqueto falsos positivos me da lo mismo, es más importante identificar aquellos pacientes que tienen cáncer. En otro sector, si estoy haciendo un modelo de fraude ojo con los falsos positivos, puedo estar perdiendo una oportunidad de negocio por etiquetar como operaciones fraudulentas aquellas que no lo son. Elegir el punto de corte no es un problema de optimización, no me habléis de punto óptimo, habladme del mejor punto para nuestros objetivos.
Voy a suspender por no haber contado este royo…
Hola Raúl.
Muy buena entrada, e instructiva, pero estoy hecho un lío, porque no me cuadra la definición de sensibilidad con la forma de calcularla: si la sensibilidad es la probabilidad de clasificar correctamente a una persona enferma, el numerador no debería ser los enfermos que han dado positivo en la prueba, y el denominador el total del grupo de enfermos (es decir, 66)?
Tanto en la página del Ramón y Cajal como aquí se calcula, por ejemplo, la sensibilidad para el punto de corte 65 como 3/34=0,088. Pero esos 34 son las personas sanas, no? La sensibilidad para ese punto de corte no sería 1/66=0,015?
Gracias por anticipado y saludos!
Vale, acabo de caer en que el grupo «sin Fe» es el grupo de «enfermos». Estaba obcecado con que el «sin» significaba «sin enfermedad», no sé por qué.
Saludos!