Primeros pasos con regresión no lineal (nls) con R

La regresión no lineal se da cuando tenemos que estimar Y a partir de una función del tipo Y=f(X,Beta) + Error donde Beta son Beta1, Beta2,…, Beta n. Unos datos X e Y se relacionan mediante una función no lineal respecto a unos parámetros Beta desconocidos. Y cómo obtenemos estos Beta desconocidos, a través de mínimos cuadrados o bien con otros métodos como máxima verosilimilitud. Este cálculo llevará asociada su inferencia estadística habitual. La función que asocia los pares de datos (x1,y1), (x2, y2),…, (yn, xn) será una función conocida. Por eso esta técnica es muy utilizada en ciencias químicas, geodinámica,… donde ya se conoce la relación que hay entre las variables independientes y la variable dependiente pero es necesario realizar modelos con los pares de datos disponibles de cara a obtener estimaciones.

Para la realización de este monográfico con R vamos a emplear el conjunto de datos Thurber Son datos de un estudio NIST de movilidad de electrones en semiconductores la variable respuesta es la movilidad del electrón y la variable regresora es el logaritmo de la densidad. El modelo es:

Nuestra variable está relacionada con su regresora por un modelo racional con siete parámetros Beta1, Beta2,…, Beta7 y cúbicas. Comenzamos el trabajo con los datos en R:

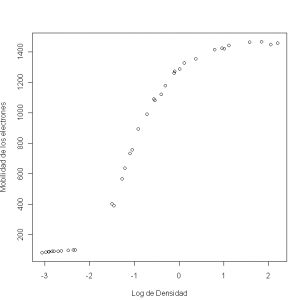
y = c(80.574 ,84.248 ,87.264 ,87.195 ,89.076 ,89.608 ,89.868 ,
90.101 ,92.405 ,95.854 ,100.696 ,101.06 ,401.672 ,390.724 ,
567.534 ,635.316 ,733.054 ,759.087 ,894.206 ,990.785 ,1090.109 ,
1080.914 ,1122.643 ,1178.351 ,1260.531 ,1273.514 ,1288.339 ,
1327.543 ,1353.863 ,1414.509 ,1425.208 ,1421.384 ,1442.962 ,
1464.35 ,1468.705 ,1447.894 ,1457.628)

x = c(-3.067 ,-2.981 ,-2.921 ,-2.912 ,-2.84 ,-2.797 ,
-2.702 ,-2.699 ,-2.633 ,-2.481 ,-2.363 ,-2.322 ,-1.501 ,-1.46 ,
-1.274 ,-1.212 ,-1.1 ,-1.046 ,-0.915 ,-0.714 ,-0.566 ,-0.545 ,
-0.4 ,-0.309 ,-0.109 ,-0.103 ,0.01 ,0.119 ,0.377 ,0.79 ,0.963 ,
1.006 ,1.115 ,1.572 ,1.841 ,2.047 ,2.2)

#Representación de los datos
plot(y ~ x,xlab="Log de Densidad",
ylab="Mobilidad de los electrones")

Metemos los datos directamente desde la web a R. Realizamos una representación gráfica de los datos y se aprecia la inexistencia de relación lineal. Se nos indica que existe relación entre las variables mediante la función antes indicada. Introduzcamos en R la función:

foo = function(x,b1,b2,b3,b4,b5,b6,b7){
(b1 + b2*x + b3*x^2 + b4*x^3)/
(1 + b5*x + b6*x^2 + b7*x^3)}

El trabajo con R le vamos a llevar a cabo con la función nls del paquete stats. Pero antes de crear un modelo de regresión no lineal tenemos que asignar unos valores iniciales a los parámetros Beta de nuestra ecuación. La regresión no lineal es un proceso iterativo. Se parte de unos parámetros Beta iniciales, se modeliza y mediante un proceso de optimización numérica se aproximan los parámetros seleccionados a los valores óptimos. Si empleamos el algoritmo de Gauss-Newton partiríamos de la mínima suma de cuadrados de los residuos (modelo lineal) y tomaríamos esta función como función a minimizar algo que es posible debido a que al menos una derivada depende de uno de los parámetros Beta (condición de no linealidad). El proceso busca mínimos locales de la función y que posteriormente habrá de comprobar si son mínimos globales hasta que el proceso llegara a converger (o no). Para obtener los valores iniciales es necesario conocer los datos. En nuestro caso tenemos una división y 7 parámetros. Vamos a observar la gráfica con los datos. Para x=0 el valor de y ha de ser muy próximo a 1200, luego ese es un buen inicio para b1. No podemos tener valores negativos, luego los parámetros que multiplican tanto a x como a x^3 no deberían ser los más altos. Además tenemos una división y luego los parámetros que estén en el denominador no deberían ser muy altos ya que la función ha de ser creciente. Si comenzamos a ejecutar:

plot(y ~ x,xlab="Log de Densidad",
ylab="Mobilidad de los electrones",main="Prueba 1")
curve(foo(x,1200,100,100,1,0.1,1,0.1),add=T,col="red")

Vemos que hasta 0 la curva no tiene mal aspecto, pero a desde ese punto la forma no es adecuada. Los parámetros del denominador pueden ser más bajos:

plot(y ~ x,xlab="Log de Densidad",
ylab="Mobilidad de los electrones",main="Prueba 2")
curve(foo(x,1200,100,100,1,-0.1,0.1,-0.1),add=T,col="blue")

Realicemos un primer modelo con estas especificaciones:

m1start=list(b1=1200,b2=100,b3=100,b4=1,b5=-0.1,b6=0.1,b7=-0.1)

Obtenemos el error Error en nlsModel(formula, mf, start, wts) : singular gradient matrix at initial parameter estimates Este error se produce debido a que los valores iniciales no son correctos para poder realizar el algoritmo inicial ya que no es posible encontrar un primer gradiente. Podríamos ir realizando diversas pruebas para encontrar los valores iniciales e incluso elaborar una parrilla de datos. También podemos emplear la librería nls2:

#install.packages("nls2")
library(nls2)
m1<- nls2(y ~ foo(x,b1,b2,b3,b4,b5,b6,b7),
start=c(b1=1200,b2=100,b3=100,b4=1,b5=-0.1,b6=0.1,b7=-0.1),
control = nls.control(warnOnly = TRUE))

Con esta librería nls2 estamos empleando el algoritmo “brute force” que se emplea para encontrar los valores iniciales. Es importante destacar que no se emplea para realizar el modelo, sólo para resolver la problemática de los valores iniciales. En este ejemplo concreto se sabe que los valores iniciales son:

B1=1000
B2=1000
B3=400
B4=40
B5=0.7
B6=0.3
B7=0.03

m.nls = nls(y ~ foo(x,b1,b2,b3,b4,b5,b6,b7),
start = c(b1 = 1000, b2 = 1000, b3 = 400, b4 = 40,
b5 = 0.7, b6 = 0.3, b7 = 0.03),trace=T)

En este caso ya hemos obtenido resultados. Con summary(m.nls) la salida obtenida es:

Formula: y ~ foo(x, b1, b2, b3, b4, b5, b6, b7)

Parameters:
Estimate Std. Error t value Pr(>|t|)
b1 1.288e+03  4.665e+00 276.141  < 2e-16 ***
b2 1.491e+03  3.957e+01  37.682  < 2e-16 ***
b3 5.832e+02  2.870e+01  20.323  < 2e-16 ***
b4 7.542e+01  5.567e+00  13.546 2.55e-14 ***
b5 9.663e-01  3.133e-02  30.840  < 2e-16 ***
b6 3.980e-01  1.499e-02  26.559  < 2e-16 ***
b7 4.973e-02  6.584e-03   7.553 2.02e-08 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 13.71 on 30 degrees of freedom

Number of iterations to convergence: 28
Achieved convergence tolerance: 8.36e-06

El algoritmo ha necesitado de 28 iteracciones, vemos los estimadores de los parámetros. Ahora es necesario que realicemos un diagnóstico del modelo. Comenzamos por graficar el resultado del modelo:

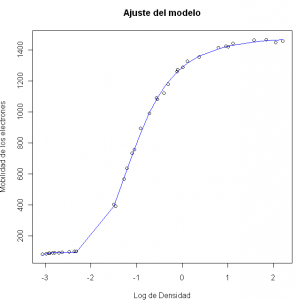
plot(y ~ x,xlab="Log de Densidad",
ylab="Mobilidad de los electrones",main="Ajuste del modelo")
lines(x,fitted(m.nls),col="blue")

Gráficamente el modelo ajusta bien. Podemos ver la suma del cuadrado de los errores con la función deviance:

deviance(m.nls)
[1] 5642.708

También es necesario analizar si el modelo cumple las hipótesis de ser estadísticamente válido con el test F, homocedasticidad, distribución normal de los errores y errores independientes. El test F lo podemos realizar con un test ANOVA con el ajuste por mínimos cuadrados frente a nuestro modelo de regresión no lineal. El código R que podemos emplear para realizar estas tareas es:

#Anova para contraste de falta de ajuste

m.lm <- lm(y~x)
anova(m.nls,m.lm)

#Independencia de los residuos
plot(fitted(m.nls),residuals(m.nls),
xlab="Valores ajustados",ylab="Residuos")
abline(a=0,b=0,col="blue")

#Test de normalidad de los residuos
qqnorm(residuals(m.nls))
qqline(residuals(m.nls))
shapiro.test(residuals(m.nls))

#Test de Leneve
library(car)
levene.test(y,as.factor(x))

#Intervalos de confianza
confint(m.nls)

No entramos en más detalles para no alargar la entrada. Pero ya disponemos de las herramientas de R para comenzar a trabajar con este tipo de modelos. También recomiendo ver las posibilidades de la librería nlstools. Saludos.