Atentos a los intervalos de confianza

Un intervalo de confianza es la zona en la que me fío de lo que estimo. Cuanto más amplia es esa zona menos me fío de lo que estimo y cuanto más estrecha más me fío de lo que estimo. Lo que pasa es que un intervalo de confianza por definición empieza con la famosa expresión “dada una población de media nu y desviación típica sigma…”

¡¡¡FU FU FU FU FU FU!!!

Cuando una definición empieza así levantad las orejas como el can que tenéis al comienzo de estas líneas, una brava infante de marina que, tras 11 años cuidando de mi y de mi familia está pasando horas bajas. Y debéis estar atentos porque estáis trabajando con una media y cuando los datos se parezcan más a la media más me fío de lo que estimo. Sin embargo no por estar más cerca de la media mi estimación tiene que ser mejor. Hacemos unos datos aleatorios con SAS:

data uno;
do x = 1 to 100;
tam = int(110 - rangam(3,x))/30;
do j = 1 to tam;
y = ranuni(8);
dist = sqrt((y-x/100)**2);
if dist

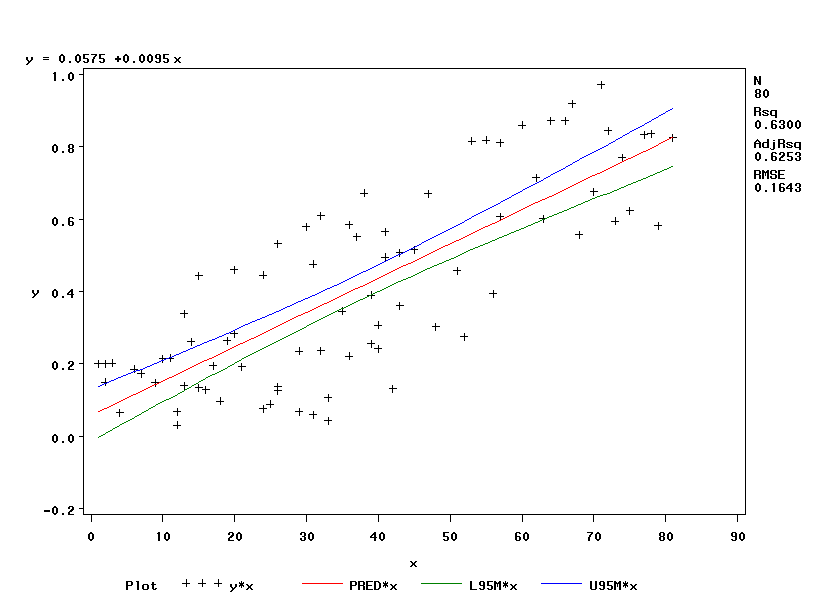
Tenemos una nube de puntos a la que deseamos ajustar un modelo de regresión lineal y obtener un intervalo de confianza:

proc reg data=uno;
model y = x/spec;
plot y*x/conf;
run;quit;

Podemos observar que el intervalo se estrecha en la zona central de nuestra recta de regresión, es decir, es más estrecho en el punto (media_y,media_x) por donde pasan todas las rectas de regresión, sin embargo casi todos los puntos están fuera de ese intervalo en esa zona y a la izquierda, donde el intervalo es ligeramente más ancho, casi todos los puntos caen dentro. No es un modelo que presenta homocedasticidad algo que comprobamos con la opción spec. Es evidente que los datos tienen poco de aleatorios, están forzados para que salga lo que tiene que salir, pero se trata de alertaros sobre medias y desviaciones típicas. Y pediros, también, que veáis gráficos de residuos cuando modelicéis:

 
proc reg data=uno;
model y = x;
plot y*x/conf;
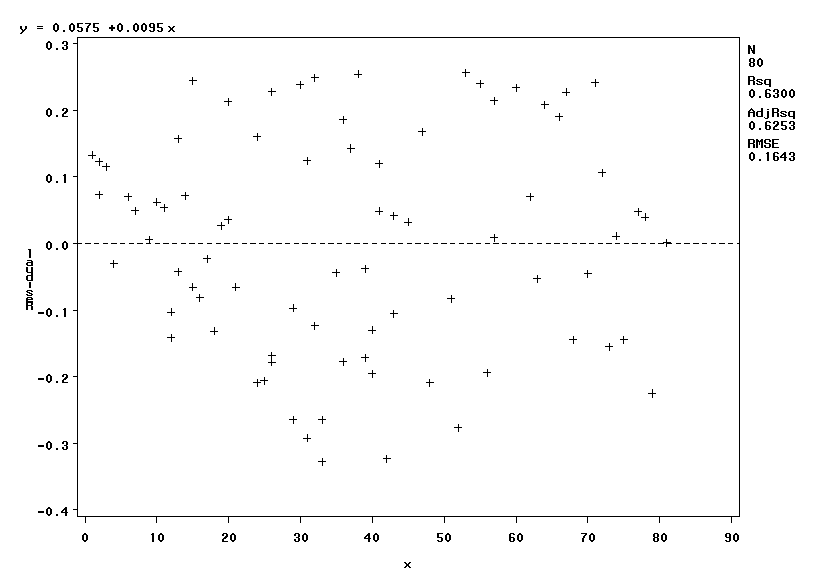
plot residual.*x;
run;quit;

A la vista de este gráfico podríamos apreciar heterocedasticidad, pero no es muy clara, pero si que es evidente que mi modelo funciona mucho mejor para valores pequeños de X, donde los intervalos de confianza eran más anchos, donde menos me fío de lo que estimo. Saludos.