Cuando clasificamos datos con SVM es necesario fijar un margen de separación entre observaciones, si no fijamos este margen nuestro modelo sería tan bueno tan bueno que sólo serviría para esos datos, estaría sobrestimando y eso es malo. El coste C y el gamma son los dos parámetros con los que contamos en los SVM. El parámetro C es el peso que le
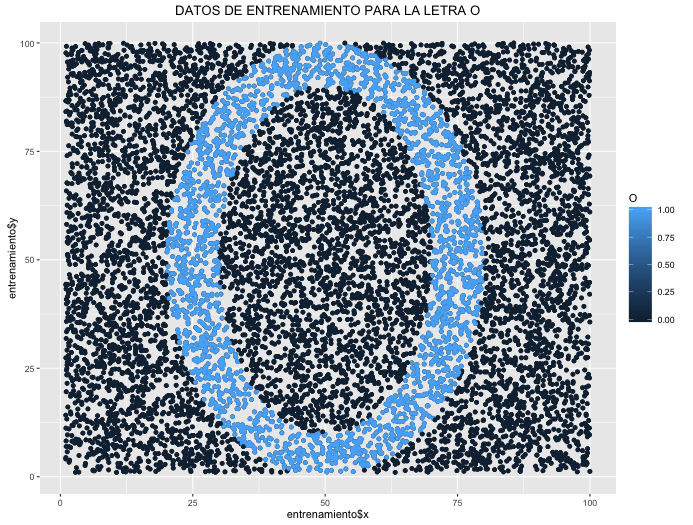
damos a cada observación a la hora de clasificar un mayor coste implicaría un mayor peso de una observación y el SVM sería más estricto (este link aclara mejor las cosas). Si tuvieramos un modelo que clasificara observaciones en el plano como una letra O podemos ver como se modifica la estimación en esta secuencia en la que se ha modificado el parámetro C:
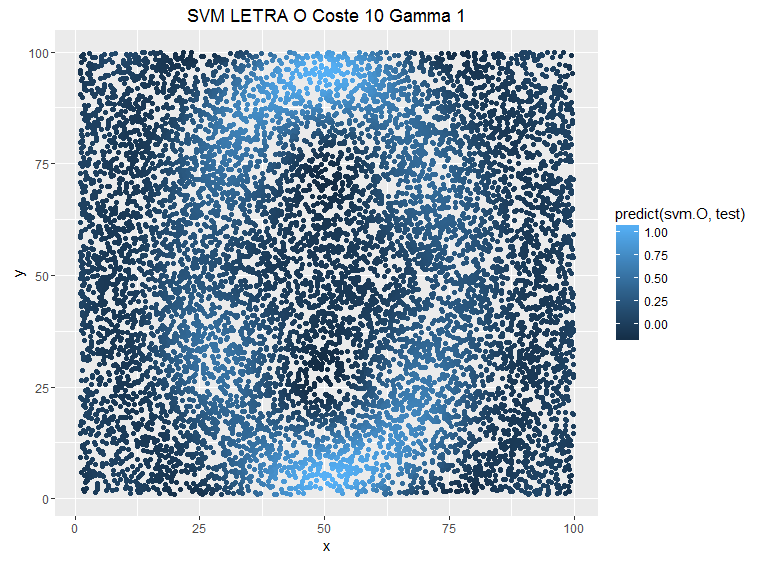
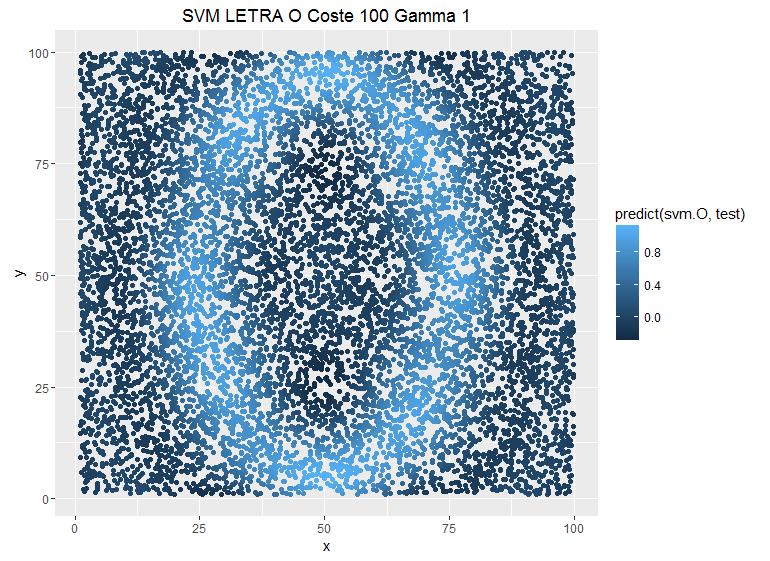
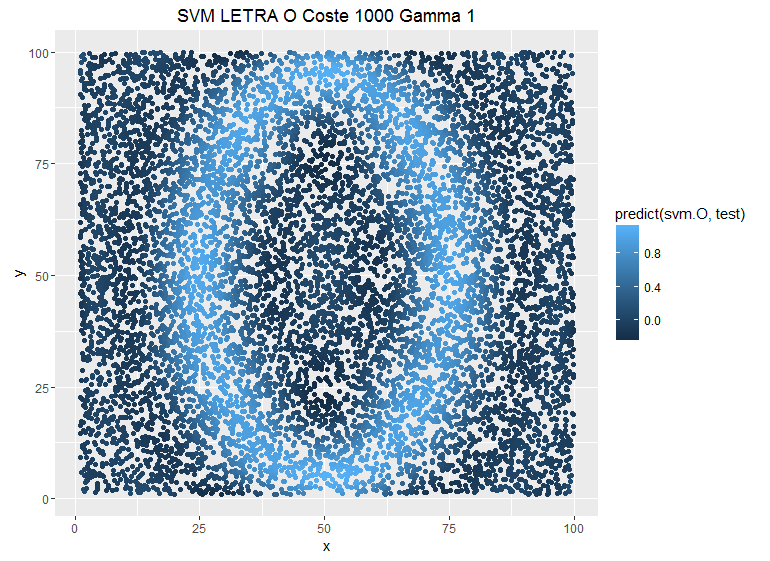
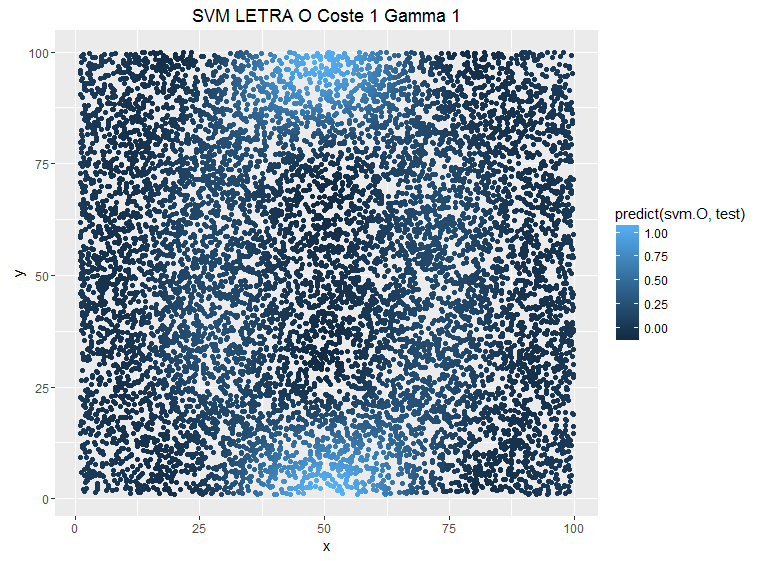
Se puede ver como la predicción es más conservadora cuando ponemos costes más bajos, pero no es el único parámetro que tenemos para suavizar la sobrestimación también tenemos el parámetro gamma que le da otra vuelta de tuerca a la relación entre las observaciones ya no es una relación entre puntos del espacio, ahora esta relación es una función kernel, lo que nos facilita encontrar los subespacios que puedan diferenciar los puntos en el espacio y también nos permite añadir mayor complejidad a la hora de separar observaciones. Veamos el ejemplo anterior pero modificando el parámetro Gamma y dejando fijo el C:
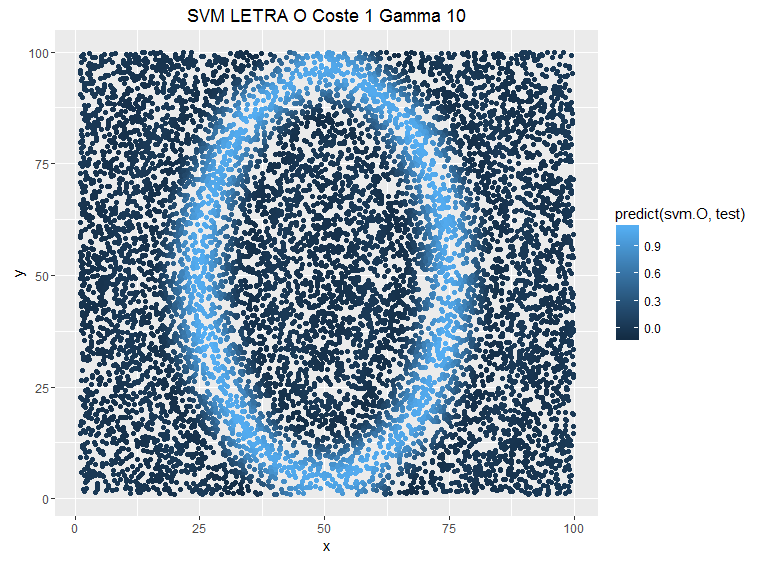
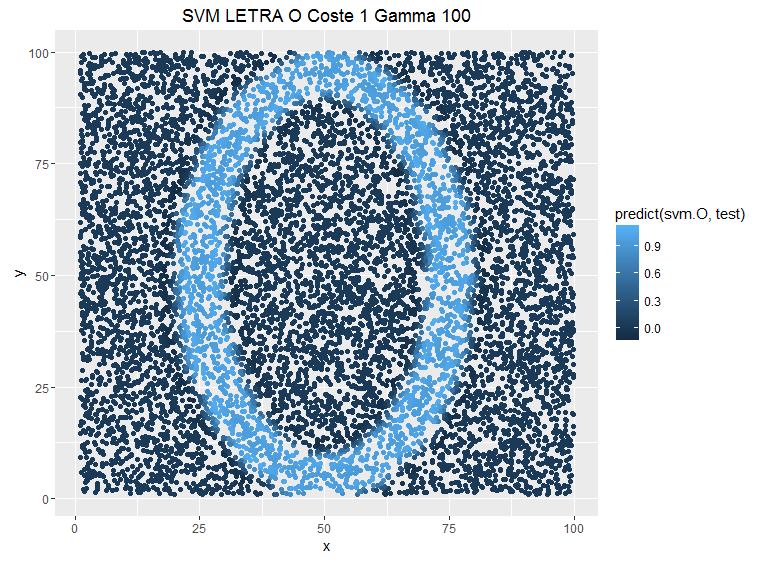
Un menor gamma implica una mayor distancia entre las observaciones que separan los subespacios del SVM luego la estimación es más conservadora, sin embargo un mayor parámetro «fastidia» a la función kernel. Si vemos la definición de esta función kernel se entiende mejor:
El ejercicio teórico es muy radical, pero también observamos como a mayor gamma las predicciones están menos suavizadas. Tenemos estos dos parámetros y la pregunta sería ¿cuál es la mejor elección? Dónde está el mejor punto para obtener un buen resultado en este trueque de sesgo-varianza. De momento no sé deciros, pero estoy con ello.
Evidentemente todo este ejercicio teórico tan radical está hecho con datos aleatorios en R, el código empleado es:
[source languaje=»R»]
library(ggplot2)
library(e1071)
#Datos iniciales
long = 20000
x <- runif(long,1,100)
y <- runif(long,1,100)
datos <- data.frame(x,y)
#La mitad entrenamiento la mitad test
indices <- sample(1:long,long/2)
entrenamiento <- datos[indices,]
test <- datos[-indices,]
#letra O
O <- ifelse((entrenamientox-50)^2/20^2 + (entrenamientoy-50)^2/40^2 >1 , 1,0)
O <- ifelse((entrenamientox-50)^2/30^2 + (entrenamientoy-50)^2/50^2 >1 , 0,O)
g.train <- ggplot(entrenamiento,aes(entrenamientox,entrenamientoy)) + geom_point()
g.train + geom_point(aes(colour = O)) + labs(title=»DATOS DE ENTRENAMIENTO PARA LA LETRA O»)
#Gráfico de test
g.test <- ggplot(test,aes(x, y)) + geom_point()
svm.O=svm(O ~ x + y,entrenamiento,method=»C-classification»,
kernel=»radial»,cost=10,gamma=1)
g.test + geom_point(aes(colour = predict(svm.O,test))) +
labs(title=»SVM LETRA O Coste 10 Gamma 1″)
svm.O=svm(O ~ x + y,entrenamiento,method=»C-classification»,
kernel=»radial»,cost=100,gamma=1)
g.test + geom_point(aes(colour = predict(svm.O,test))) +
labs(title=»SVM LETRA O Coste 100 Gamma 1″)
svm.O=svm(O ~ x + y,entrenamiento,method=»C-classification»,
kernel=»radial»,cost=1000,gamma=1)
g.test + geom_point(aes(colour = predict(svm.O,test))) +
labs(title=»SVM LETRA O Coste 1000 Gamma 1″)
##########################################################################
svm.O=svm(O ~ x + y,entrenamiento,method=»C-classification»,
kernel=»radial»,cost=1,gamma=1)
g.test + geom_point(aes(colour = predict(svm.O,test))) +
labs(title=»SVM LETRA O Coste 1 Gamma 1″)
svm.O=svm(O ~ x + y,entrenamiento,method=»C-classification»,
kernel=»radial»,cost=1,gamma=10)
g.test + geom_point(aes(colour = predict(svm.O,test))) +
labs(title=»SVM LETRA O Coste 1 Gamma 10″)
svm.O=svm(O ~ x + y,entrenamiento,method=»C-classification»,
kernel=»radial»,cost=1,gamma=100)
g.test + geom_point(aes(colour = predict(svm.O,test))) +
labs(title=»SVM LETRA O Coste 1 Gamma 100″)
[/source]