El sobremuestreo (oversampling) es una técnica de muestreo que se emplea habitualmente cuando tenemos una baja proporción de casos positivos en clasificaciones binomiales. Los modelos pueden “despreciar” los casos positivos por ser muy pocos y nuestro modelo no funcionaría. Para incrementar el número de casos positivos se emplea el sobremuestreo. Ejemplos habituales pueden ser los modelos de fraude, un 99% de las compras son correctas, un 1% son fraudulentas. Si realizo un modelo puedo estar seguro al 99% de que todas mis compras son correctas, en este caso hemos de realizar un sobremuestreo para incrementar nuestros casos de fraude y poder detectar los patrones.
Personalmente no sabría deciros el porcentaje de casos positivos a partir del cual sería necesario llevar a cabo un proceso de remuestreo. A mi particularmente me gusta hacerlo siempre. Por lo menos realizar algunas pruebas para identificar aquellas variables que son más influyentes y comenzar a eliminar aquellas que no van a funcionar. Busco exagerar. Tampoco me quiero mojar mucho sobre la proporción de casos positivos y negativos, pero si estamos realizando un nuevo muestreo podemos emplear perfectamente un 50% para ambos, aquí si que dependemos del número de registros con el que estemos trabajando ya que al final el sobremuestreo será la repetición de los casos positivos sobre la tabla de entrada del modelo.
Sin embargo, cuando ya tengo decidido como va a ser mi modelo no me gusta realizar sobremuestreo. Lo considero un paso previo (algún lector del blog considerará estas palabras incoherentes). Después de toda esta exposición teórico-práctica de malos usos de un dinosaurio en realidad lo que cabepreguntarse es ¿mejora la estimación un modelo con sobremuestreo?
Abrimos R y Tinn-R y manos a la obra. Datos simulados de una entidad bancaria que desea realizar un modelo para realizar una campaña comercial sobre renta o Pensión Vitalicia Inmediata (PVI) conocidos por todos:
clientes=20000
saldo_vista=runif(clientes,0,1)*10000
saldo_ppi=(runif(clientes,0.1,0.6)*rpois(clientes,2))*60000
saldo_fondos=(runif(clientes,0.1,0.9)*(rpois(clientes,1)-0.5>0))*30000
edad=rpois(clientes,60)
datos_ini<-data.frame(cbind(saldo_vista,saldo_ppi,saldo_fondos,edad))
datos_inisaldo_ppi=(edad<65)*datos_inisaldo_ppi
#Creamos la variable objetivo a partir de un potencial
datos_inipotencial= runif(clientes,0,1)
datos_inipotencial= datos_inipotencial + log(edad)/2 + runif(1,0,0.03)*(saldo_vista>5000)+runif(1,0,0.09)*(saldo_fondos>5000)+runif(1,0,0.07)*(saldo_ppi>10000)
summary(datos_ini)
datos_inipvi=as.factor((datos_inipotencial>=quantile(datos_inipotencial,
0.98))*1)
#Eliminamos la columna que genera nuestra variable dependiente
datos_ini = subset(datos_ini, select = -c(potencial))
#Realizamos una tabla de frecuencias
table(datos_ini$pvi)
Sólo encontramos un 2% de casos positivos de los 20.000 clientes analizados. Para nuestro pequeño estudio vamos a emplear regresión logística y árboles de decisión, pero lo primero que vamos a hacer es seleccionar una parte de las observaciones para validar los modelos realizados:
#Subconjunto de validacion
validacion <- sample(1:clientes,5000)
Estos 5.000 clientes no entrenarán ningún modelo sólo validarán los modelos, con y sin sobremuestreo, que realicemos. Vamos a generar la muestra con un porcentaje del 50% de casos positivos mediante la librería de R sample:
#install.packages("sampling")
library( sampling )
#Muestra estratificada aleatoria con reemplazamiento de tamaño 10000
selec1 <- strata( datos_ini[-validacion,], stratanames = c("pvi"),
size = c(5000,5000), method = "srswr" )
Con strata realizamos el muestreo estratificado, el estrato es nuestra variable dependiente y así lo indicamos en stratanames, como tenemos 2 estratos en size indicamos 5000 observaciones para cada uno de ellos y el método srswr señala que es muestreo con reemplazamiento (with replacement).
Modelo de regresión logística:
#Modelo sin sobremuestreo
modelo.1 = glm(pvi~.,data=datos_ini[-validacion,],family=binomial)
summary(modelo.1)
#Modelo con sobremuestreo
#Nos quedamos con el elemento ID_unit
selec1 <- selec1$ID_unit
modelo.2 = glm(pvi~.,data=datos_ini[selec1,],family=binomial)
summary(modelo.2)
Ambos modelos convergen, tienen parámetros similares y las inferencias sobre ellos son iguales. ¿Qué modelo funciona mejor? La librería ROCR nos permite realizar curvas ROC muy empleadas para medir el comportamiento de los modelos realizados. No entramos en detalle sobre el código para no alargar esta entrada:
#Realizamos la curva ROC para ambos modelos y comparamos
#install.packages("ROCR")
library(ROCR)
#Objeto que contiene la validación del modelo sin sobremuestreo
valida.1 <- datos_ini[validacion,]
valida.1pred <- predict(modelo.1,newdata=valida.1,type="response")
pred.1 <- prediction(valida.1pred,valida.1pvi)
perf.1 <- performance(pred.1,"tpr", "fpr")
#Validación con sobremuestreo
valida.2 <- datos_ini[validacion,]
valida.2pred <- predict(modelo.2,newdata=valida.2,type="response")
pred.2 <- prediction(valida.2pred,valida.2pvi)
perf.2 <- performance(pred.2,"tpr", "fpr")
#Pintamos ambas curvas ROC
plot(perf.2,colorize = FALSE)
par(new=TRUE)
plot(c(0,1),c(0,1),type='l',col = "red",
lwd=2, ann=FALSE)
par(new=TRUE)
plot(perf.1,colorize = TRUE)
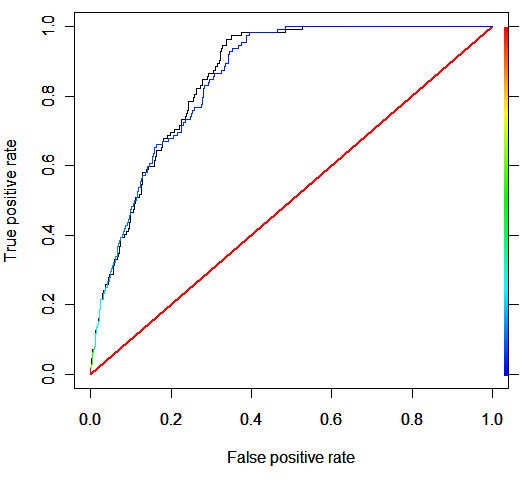
La línea negra es el modelo con sobremuestreo y presenta una ligera (muy ligera mejora con respecto al modelo sin sobremuestreo). Para la regresión logística y en este ejemplo el modelo con sobremuestreo no mejora al modelo sin sobremuestreo.
Modelos con árboles de decisión:
library(rpart)
#Modelo sin sobremuestreo
arbol.1=rpart(as.factor(pvi)~edad+saldo_ppi+saldo_fondos,
data=datos_ini[-validacion,],method="anova",
control=rpart.control(minsplit=20, cp=0.001) )
#Modelo con sobremuestreo
arbol.2=rpart(as.factor(pvi)~edad+saldo_ppi+saldo_fondos,
data=datos_ini[selec1,],method="anova",
control=rpart.control(minsplit=20, cp=0.001) )
#Validacion sin sobremuestreo
valida.arbol.1 <- datos_ini[validacion,]
valida.arbol.1pred <- predict(arbol.1,newdata=valida.arbol.1)
pred.1 <- prediction(valida.arbol.1pred,valida.arbol.1pvi)
perf.1 <- performance(pred.1,"tpr", "fpr")
#Validacion con sobremuestreo
valida.arbol.2 <- datos_ini[validacion,]
valida.arbol.2pred <- predict(arbol.2,newdata=valida.arbol.2)
pred.2 <- prediction(valida.arbol.2pred,valida.arbol.2pvi)
perf.2 <- performance(pred.2,"tpr", "fpr")
#Pintamos ambas curvas ROC
plot(perf.2,colorize = FALSE)
par(new=TRUE)
plot(c(0,1),c(0,1),type='l',col = "red",
lwd=2,ann=FALSE)
par(new=TRUE)
plot(perf.1,colorize = TRUE)
Analizamos el gráfico resultante:
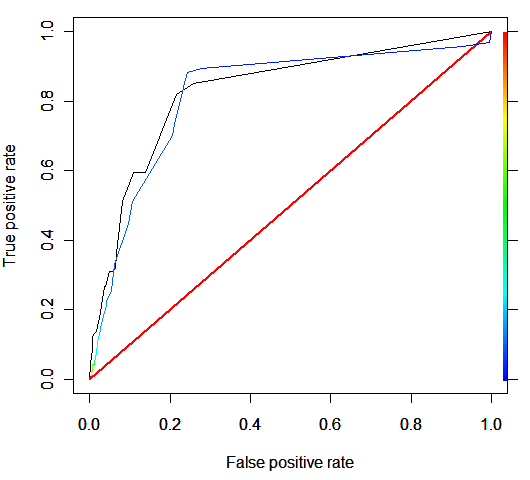
En este caso las curvas ROC son distintas y os dejo que saquéis vuestras propias conclusiones y las comentéis en el blog. Para evitarós problemas os dejo en este enlace el código empleado para este experimento. Ejecutadlo para analizar los resultados.
Hola, me parece muy útil esta entrada, aunque hay conceptos que no llego a entender. Echando un vistazo a tus anteriores entradas (como https://analisisydecision.es/muestreo-de-datos-con-r/), me doy cuenta que tengo que refrescar conceptos estadísticos (hace mucho que acabe la facultad). ¿Recomendarías algún libro para refrescar conceptos (metodologias de muestreos, intervalos de confianza, etc..)?. Muchas gracias.
Hola a todos;
interesante entrada, toca un tema que se da muy por supuesto y casi no he visto expuesto en ningún sitio.
Yo lo que tiendo a hacer es quedarme con todos los casos posivitos y muestreo lo negativos, empezando por una proporción 50/50, y a partir de allí voy creado muestras de entreno con diferentes % 40/60, 30/70 … a mí normalmente me funciona muy bien y me curo en salud a la hora de repetir patrones positivos de forma aleatoria.
No se si tiene una base teorica o es una burrada y un mal vicio pero como hasta ahora la cosa va no me he planteado cambiar…
¿Qué pensais?
El sobremuestreo es una práctica muy extendida, sin embargo a todos nos da «vergüenza» confesarlo. De hecho teóricamente no debería mejorar mi estimación, pero el que esté libre de pecado…
Tengo una propuesta para «solventar» el problema. Asignar a los registros de casos negativos un peso menor en la estimación, de esta manera no hay que elegir aleatoriamente registros, si no que entran todos con un peso menor.
Por ejemplo, en un modelo de riesgo de impago, cada registro de moroso cuenta como frecuencia=1 y cada registro de sano cuenta como frecuencia=0.05.
Luego haríamos, sigue siendo ejemplo
weight frecuencia;
en la logística, o lo que estemos usando y ya lo tendrá en cuenta para ver el más verosímil (o el criterio que pongamos).
¿No puede ser?
Saludos
Parece que no he tenido mucho éxito.
¿Es una burrada lo que digo?.
Yo lo he probado y diría que funciona.
Perdón por no contestarte Roberto. Esta semana haré una entrada en el blog al respecto.