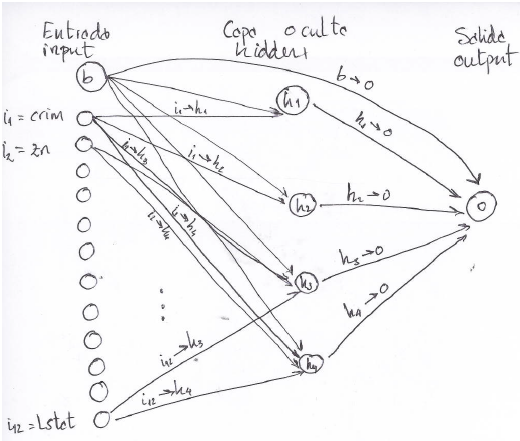
En la última entrada realizamos un modelo de regresión con redes neuronales. Hoy quería mostraros como representar gráficamente la red neuronal creada en esa entrada. A la modelización con redes neuronales siempre se le ha achacado un comportamiento de “caja negra”, nosotros pasamos unas variables de entrada por una capa oculta y obtenemos una salida. No hay parámetros ni inferencia sobre los mismos, no sabemos lo que hace la red por dentro. En el caso concreto de R y continuando con la entrada anterior si hacemos summary(bestnn):
a 12-4-1 network with 57 weights
options were – linear output units decay=1e-05
b->h1 i1->h1 i2->h1 i3->h1 i4->h1 i5->h1 i6->h1 i7->h1 i8->h1 i9->h1
-5.61 -3.80 -1.03 0.74 -2.81 2.83 2.37 2.86 6.72 4.68
i10->h1 i11->h1 i12->h1
1.65 0.87 -8.16
b->h2 i1->h2 i2->h2 i3->h2 i4->h2 i5->h2 i6->h2 i7->h2 i8->h2 i9->h2
12.05 -4.55 10.85 0.45 -0.35 -2.58 -5.59 -1.73 1.13 -2.02
i10->h2 i11->h2 i12->h2
-1.46 3.18 -4.31
b->h3 i1->h3 i2->h3 i3->h3 i4->h3 i5->h3 i6->h3 i7->h3 i8->h3 i9->h3
2.82 0.78 -0.03 0.03 0.08 -0.54 0.25 0.34 0.06 0.48
i10->h3 i11->h3 i12->h3
0.20 0.12 0.09
b->h4 i1->h4 i2->h4 i3->h4 i4->h4 i5->h4 i6->h4 i7->h4 i8->h4 i9->h4
-11.34 -0.80 2.27 1.15 -4.63 0.05 1.52 -8.82 1.74 1.13
i10->h4 i11->h4 i12->h4
-0.60 0.12 -2.18
b->o h1->o h2->o h3->o h4->o
1.46 0.10 0.12 -1.26 0.61
Eso es (mas o menos) lo que hay pintado en el dibujo de arriba. 12 nodos de entrada (input) más el sesgo (bias). Luego tenemos 4 nodos en la capa oculta (hidden), en este caso me falta el sesgo. Con nnet sólo podemos realizar redes con una sola capa oculta. Y por último una sola de salida (output) porque estamos realizando una regresión, no una clasificación. Con ello nnet siempre usa la notación b->h1; i1->h1;…;b->o;h1.->o para los pesos de la red neuronal. Estos pesos harán de parámetros de nuestros modelos, en nuestro caso concreto tenemos 12-4-1 input-hidden-output 12×4=48 (i->h) + 4 (b->h) + 4 (b->o) + 1 (b->o) = 57 pesos. Con un modelo 3-4-2 tendríamos 3×4 + 4 + 4 + 2 = 22 pesos. Pues interpretar estas salidas para ayudarnos a comprender mejor el comportamiento predictor de nuestras variables de entrada es una tarea complicada a no ser que realizáramos un gráfico. Para graficar este tipo de redes neuronales tenemos obligatoriamente que leer esto:
http://beckmw.wordpress.com/2013/11/14/visualizing-neural-networks-in-r-update/
Un genio. Desde aquí mi felicitación. ¡¡¡OOOOOLE!!!
source(url(‘https://gist.githubusercontent.com/fawda123/7471137/raw/466c1474d0a505ff044412703516c34f1a4684a5/nnet_plot_update.r’))
plot.nnet(bestnn)
Y tenemos el siguiente gráfico:
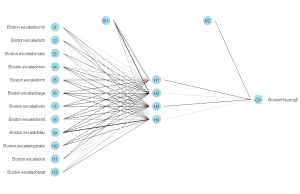
Líneas negras implican pesos positivos, cuanto más anchura de la línea más peso. Líneas grises implican pesos negativos. Esto podemos cambiarlo:
plot.nnet(bestnn,pos.col=»blue»,neg.col=»red»)
Tiene muchas posibilidades como podemos ver en la entrada del blog. El código está al alcance de nuestra mano:
plot.nnet node.labs=T,var.labs=T,x.lab=NULL,y.lab=NULL,line.stag=NULL,struct=NULL,cex.val=1,
alpha.val=1,circle.col='lightblue',pos.col='black',neg.col='grey', max.sp = F, ...){
Como me gusta R.
Hola Raul, quería hacerte una consultilla sobre R.
Estoy buscando documentación y librerías apropiadas para hacer visual analytics con R,
me refiero a gráficos del tipo:
– Descubrimientos de conexiones. Redes de conexiones (del tipo de las visualizaciones que se muestran para ver como se conectan usuarios en el uso del móvil, grupos de usuarios con llamadas frecuentes entre sí).
– Mapas de calor
– Histogramas 2D
– gráficos en coordenadas polares
– Todo tipo de gráfico que ayude a encontrar relaciones o patrones.
Mirate el paquete igraph y ggplot2. Con esos dos paquetes tienes resuelto ese tipo de gráficos. Saludos.
Muchas gracias, Raul
Hola Raul, muy interesante la representación gráfica de la red, esto ni Miner lo hace, quedé gratamente sorprendido. Tengo una duda es posible interpretar los pesos positivos como aumento positivo en la variable respuesta? tengo la duda de la salida de las capas ocultas. Lo que personalmente hago para entender una red es predecir mediante un arbol la variable que anteriormente predijo la red ( no se si me haga entender) y de esta manera ver que variables implican una Predicción superior e inferior.
y tambien te quería preguntar como hago para reproducir la capa de salida de la red en el siguiente caso en donde quiero predecir una variable dicotomica.
La red tiene 3 nodos de entrada y 1 capa oculta con los siguientes pesos:
b->h1 i1->h1 i2->h1 i3->h1
0.30 5.84 -0.45 -0.71
b->o h1->o
2.67 -6.68
el código usado es
nnet(VIDA_INDIVIDUAL_TOT~INGRESOS.0A1.NOREPORTA.NOTIENE+INGRESOS.3A5+PRIMA.SALUD.MAS.2,data=BASE.MODELO[s==1,], size=1, rang = 0.1,decay = 5e-4, maxit = 200)
En si lo que quiero es poner en producción esta red en SQL, (la red que pongo es un ejemplo sencillo para saber que funciones de impulso usa R por defecto).
Muchas gracias
Hola Nicolás, en cuanto a la primera duda que planteas voy a realizar una entrada en el blog. En cuanto a la segunda la tendrás que programar en SQL.
Gracias Raul, efectivamente lo tengo que programar en SQL, pero no se las funciones de activacion que R utiliza , me podrias ayudar con el ejemplo a sacar la predicción?
Ya resolví mi duda, R usa logit como función de activación, lo que no se es si se pueda cambiar por tanh por ejemplo
Pingback: Como salva la linealidad una red neuronal | Análisis y Decisión
¡¡¡OOOOOLE!!!
Buenas tardes.
Cómo se quitan los valores de los pesos de una gráfica?
Gracias